Світ сповнений руху. Ми часто говоримо, що пройшли якусь кількість кілометрів, сплачуємо штрафи за перевищення швидкості та вибираємо найшвидший маршрут у навігаторі. Давайте вчитися його характеризувати.
Механічний рух
Коли ми йдемо до школи або на роботу, автобус під’їжджає до зупинки або солодкий коргі гуляє з господарем, ми маємо справу з механічним рухом.
Механічним рухом називається зміна положення тіл у просторі щодо інших тіл з часом.
«Щодо інших тіл» — дуже важливі слова у цьому визначенні. Для опису руху нам потрібні:
- тіло відліку
- система координат
- годинник
У сукупності ці три параметри утворюють систему відліку.
У механіці є такий розділ – кінематика. Він відповідає питанням, як рухається тіло. Далі ми з допомогою кінематики опишемо різні види механічного руху. Не перемикайтеся.
Прямолінійний рівномірний рух
Рух прямою, у якому тіло проходить рівні ділянки шляху за рівні проміжки часу називають прямолінійним рівномірним. Це будь-який рух із постійною швидкістю.
Наприклад, якщо у вас обмеження швидкості на дорозі 60 км/год, і у вас немає жодних перешкод на шляху – швидше за все, ви рухатиметеся прямолінійно рівномірно.
Ми можемо охарактеризувати цей рух такими величинами.
Скалярні величини (визначаються лише значенням)
- Час — у міжнародній системі одиниць СІ вимірюється в секундах [с].
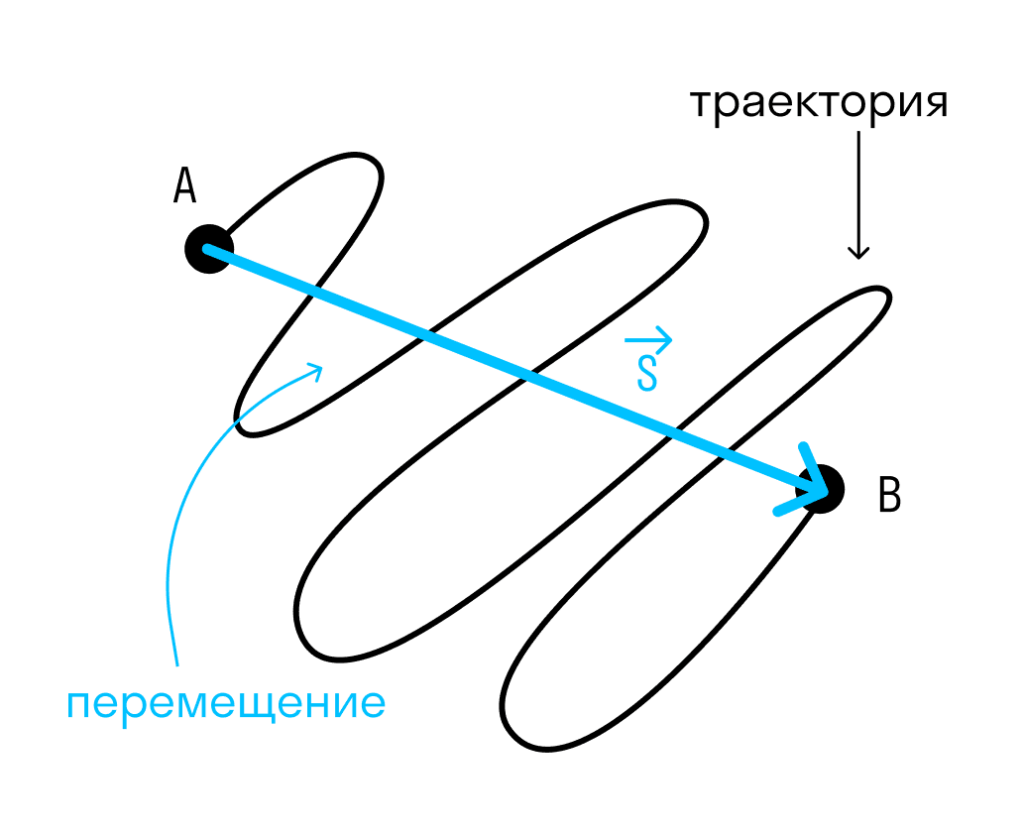
- Шлях — довжина траєкторії (лінії, якою рухається тіло). У разі прямолінійного рівномірного руху – довжина відрізка [м].
Векторні величини (визначаються значенням та напрямком)
- Швидкість — характеризує швидкість переміщення та напрямок руху матеріальної точки [м/с].
- Переміщення – вектор, проведений з початкової точки шляху до кінцевої [м].
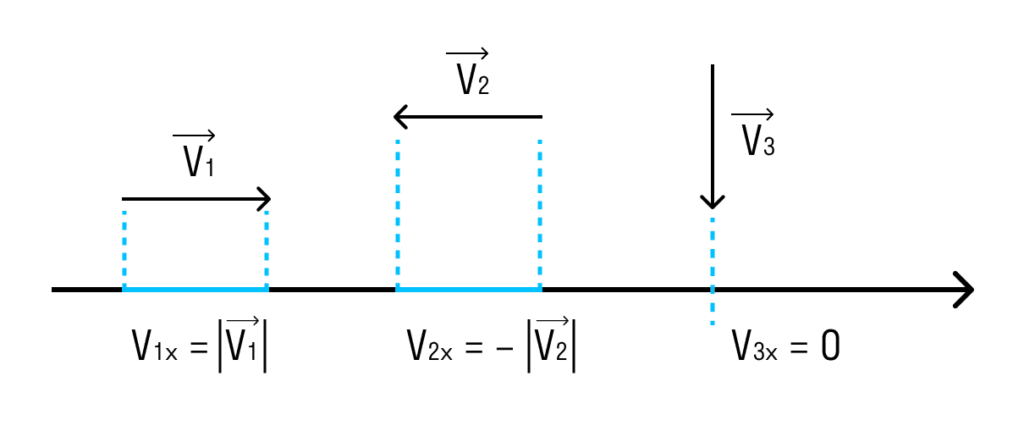
Проеціювання векторів
Векторний опис руху корисний, тому що на одному кресленні завжди можна зобразити багато різноманітних векторів і отримати перед очима наочну «картину» руху.
Однак щоразу використовувати лінійку та транспортир, щоб робити дії з векторами, дуже трудомістко. Тому ці дії зводять до дій із позитивними та негативними числами – проекціями векторів.
| Якщо вектор співнаправлений з віссю, його проекція дорівнює довжині вектора. Якщо вектор протилежно спрямований осі — проекція чисельно дорівнює довжині вектора, але негативна. Якщо вектор перпендикулярний – його проекція дорівнює нулю. |
Швидкість може визначатися за вектором переміщення та шляху, тільки це будуть дві різні характеристики.
Швидкість – це векторна фізична величина, яка характеризує швидкість переміщення, а середня шляхова швидкість – це відношення довжини шляху до часу, протягом якого шлях був пройдений.
Швидкість \vec{V} = \frac{\vec{S}}{t}V — швидкість [м/с] |
| Середня шляхова швидкість V ср. шляхова = S/t V ср. шляхова — середня дорожня швидкість [м/с] |
У чому різниця між переміщенням та шляхом?
Переміщення — це вектор, проведений з початкової точки до кінцевої, а шлях — це довжина траєкторії.
Завдання
Знайдіть, з якою середньою дорожньою швидкістю повинен рухатися автомобіль, якщо відстань від А до Б 210 кілометрів йому потрібно пройти за 2,5 години. Відповідь дайте у км/год.
Рішення:
Візьмемо формулу середньої колійної швидкості
V ср. шляхова = S/t
Підставимо значення:
V ср.шляхова = 210/2,5 = 84 км/год
Відповідь: автомобіль буде рухатися із середньою дорожньою швидкістю рівною 84 км/год
Рівняння руху
Однією з основних задач механіки є визначення положення тіла щодо інших тіл на даний момент часу. Для вирішення цього завдання допомагає рівняння руху, тобто залежність координати тіла від часу х = х(t).
| Рівняння руху x(t) = x0 + vxt x(t) – шукана координата в момент часу t [м] |
Якщо позитивний напрямок осі ОХ протилежний напряму руху тіла, то проекція швидкості тіла на вісь ОХ негативна, швидкість менша за нуль (v < 0), і тоді рівняння руху набуває вигляду:
| Рівняння руху під час руху проти осі x(t) = x0 − vxt x(t) – шукана координата в момент часу t [м] |
Прямолінійний рівноприскорений рух
Щоб розібратися з тим, що за типом руху в цьому заголовку, потрібно ввести нове поняття — прискорення.
Прискорення – векторна фізична величина, що характеризує швидкість зміни швидкості. У міжнародній системі одиниць СІ вимірюється у метрах, поділених на секунду у квадраті.
СІ – міжнародна система одиниць. “Перекласти в СІ” означає переведення всіх величин в метри, кілограми, секунди та інші одиниці виміру без приставок. Виняток – кілограм з приставкою «кіло».
Отже, рівноприскорений прямолінійний рух – це рух із прискоренням по прямій лінії. Рух, у якому швидкість тіла змінюється на рівну величину за рівні проміжки часу.
Рівняння руху і формула кінцевої швидкості
Основне завдання механіки не змінилося по ходу тексту — визначення положення тіла щодо інших тіл в даний момент часу. У рівноприскореного руху у рівнянні утворюється прискорення.
| Рівняння рівноприскореного руху x(t) = x0 + v0xt + axt2/2 x(t) — шукана координата в момент часу t [ м] |
Для цього процесу також важливо вміти знаходити кінцеву швидкість – вирішувати завдання так простіше. Кінцева швидкість знаходиться за формулою:
Формула кінцевої швидкості \vec{v} = \vec{v_0} + \vec{a}tv — кінцева швидкість тіла [м/с] v0 — початкова швидкість тіла [м/с] t — час [с] a — прискорення [м/с2] |
Завдання
Знайдіть місце розташування автобуса, який розігнався до швидкості 60 км/год за 3 хвилини, через 0,5 години після початку руху з початку координат.
Рішення:
Спершу знайдемо прискорення автобуса. Його можна виразити з формули кінцевої швидкості:
v = v_0 + at
a = \frac{v - v_0}{t}Оскільки автобус рухався з місця, v0=0 . Значить
a = \frac{v}{t}Час дано в хвилинах, переведемо в годинни, щоб співвідносилося з одиницями вимірювання швидкості.
3 хвилини = 3/60 години = 1/20 години = 0,05 години
Підставимо значення:
a = v/t = 60/0,05 = 1200 км/год2
Тепер візьмемо рівняння руху.
x(t) = x0 + v0xt + axt2/2
Початкова координата дорівнює нулю, початкова швидкість, як ми з’ясували — теж. Значить рівняння набуде вигляду:
x(t) = \frac{a_{x}t^2}{2}Прискорення ми щойно знайшли, а ось час буде не 3 хвилинам, а 0,5 години, тому що нас просять знайти координату в цей момент часу .
Підставимо циферки:
x = 1200 \cdot \frac{0,5^2}{2} = \frac{1200 \cdot 0,5^2}{2} = 150 кмВідповідь: через півгодини координата автобуса дорівнюватиме 150 км.
Рух по вертикалі
Рух по вертикалі – це окремий випадок рівноприскореного руху. Річ у тім, що Землі тіла падають з однаковим прискоренням — прискоренням вільного падіння. Для Землі воно приблизно дорівнює 9,81 м/с2, а в завданнях ми взагалі осміливаемся округляти його до 10 (фізики просто зухвалі).
Загалом у значенні прискорення вільного падіння для Землі дуже багато знаків після коми. У школі зазвичай дають значення: g = 9,8 м/с2. В іспитах ЗНО у довідкових даних дають g = 10 м/с2.
І кому ж вірити? Все просто: для кого вирішується завдання, той головний. В іспитах беремо g = 10, у школі при розв’язанні задач (якщо за умови завдання не написано щось інше) беремо g = 9,8 м/с2.
Приватним випадком руху по вертикалі (приватним випадком окремого випадку, виходить) вважається вільне падіння — це рівноприскорений рух під дією сили тяжкості, коли інші сили, що діють на тіло, відсутні або зневажливо малі.
Пам’ятайте, що вільне падіння – це не завжди рух по вертикалі зі стану спокою. Якщо ми кидаємо тіло вгору, то початкова швидкість, звичайно ж, буде.