Якщо ви візьмете гумову кульку і кулю з каменю і почнете кидати в стіну (нудний день видався, мало) – помітите, що вони відштовхуються по-різному. Про силу пружності, яка пояснює цей процес — у цій статті.
Сила: що це за величина
У повсякденному житті ми часто зустрічаємо, як будь-яке тіло деформується (змінює форму чи розмір), прискорюється чи сповільнюється, падає. Загалом чого тільки з різними тілами в реальному житті не відбувається. Причиною будь-якої дії чи взаємодії є сила.
Сила — це фізична векторна величина, яка є мірою дії одного тіла на інше.
Вона вимірюється в ньютонах. це одиниця виміру названа на честь Ісаака Ньютона.
Сила – величина векторна. Це означає, що, крім модуля, вона має напрямок. Від того, куди спрямована сила, залежить результат дії цієї сили.
От ви стоїте на лонгборді: можете відштовхнутися вправо, а можете вліво — залежно від того, в який бік відштовхнетеся, результат буде різним. В даному випадку результат виражається в напрямку руху.

Деформація
Деформація — це зміна форми та розмірів тіла (або частини тіла) під дією зовнішніх сил.
Відбувається деформація через різних факторів: при зміні температури, вологості, фазових перетвореннях і інших впливах, що викликають зміну положення частинок тіла.
На появу того чи іншого виду деформації великий вплив має характер прикладених до тіла сил. Одні процеси деформації пов’язані з переважно перпендикулярно (нормально) прикладеною силою, а інші — переважно з силою, що додається за дотичною.
За характером прикладеного до тіла навантаження види деформації поділяють так:
- Деформація розтягування
- Деформація стиснення
- Деформація зсуву
- Деформація при крученні
- Деформація при згині
Сила пружності: Закон Гука
Давайте займемося баскетболом. Почнемо набивати м’яч об підлогу, він чудово відскакуватиме. Цей удар можна назвати пружним. Якщо при ударі деформації не буде зовсім, то він буде називатися абсолютно пружним.
Якщо ви переплутали м’яч і взяли пластиліновий, він деформується при ударі і не відштовхнеться від підлоги. Такий удар буде називатися абсолютно непружним.
Деформацію теж можна назвати пружною (при якій тіло прагне повернути свою форму і розмір у початковий стан) і непружною (коли тіло не може повернутися у вихідний стан).
При деформації виникає сила пружності — це та сила, яка прагне повернути тіло у вихідний стан, в якому воно було до деформації. тіла.
Сила пружності, що виникає при пружній деформації розтягування або стиснення тіла, пропорційна абсолютному значенню зміни довжини тіла. Вираз, який описує цю закономірність, називається законом Гука.
Якою літерою позначається сила пружності?
| Закон Гука Fпр=kx Fпр — сила пружності [Н] k — коефіцієнт жорсткості [Н/м] х — зміна довжини (деформація) [м] |
Важливо раз
Зміна довжини може бути різною в різних джерелах.
Варіанти позначень: x, ∆x, ∆l.
Це рівноцінні позначення можна використовувати будь-яке зручне.
Важливо два
Оскільки сила пружності завжди спрямована проти деформації (вона прагне все «розпрямити»), в Законі Гука повинен бути знак мінус. Часто його можна зустріти в різних підручниках. Але оскільки ми враховуємо напрямок цієї сили при розв’язанні задач, знак мінус можна не ставити. м при рівномірному (без прискорення) піднятті вгору риби вагою 300 г?
Рішення:
Спочатку визначимо силу важкості. Не забуваємо масу уявити в одиницях СІ – кілограмах.
СІ – міжнародна система одиниць. “Перекласти в СІ” означає переведення всіх величин в метри, кілограми, секунди та інші одиниці виміру без приставок. Виняток становить кілограм із приставкою «кіло».
m = 300 г = 0,3 кг
Якщо прийняти прискорення вільного падіння рівним 10 м/с*с, то модуль сили тяжіння дорівнює :
F = mg = 0 ,3*10 = 3 Н.
Згадаймо закон Гука:
F=kx
І висловимо з нього модуль подовження волосіні:
x=\frac{F}{k}Оскільки одна сила врівноважує іншу, ми можемо їх прирівняти:
Fт=Fпр
Підставимо числа, жорсткість волосіні при цьому виражаємо в ньютонах:
x=\frac{3}{0,3*1000}= 0,01 м = 1 смВідповідь: Подовження волосіні дорівнює 1 см .
Паралельне та послідовне з’єднання пружин
У Законі Гука є така величина, як коефіцієнт жорсткості— це характеристика тіла, яка показує його здатність чинити опір деформації. Що коефіцієнт жорсткості, то більша ця здатність, а як наслідок із Закону Гука — і сила пружності.
Найчастіше ця характеристика використовується для опису жорсткості пружини. Але якщо ми з’єднаємо кілька пружин, то їхня сумарна жорсткість потрібно буде розрахувати. Розберемося, яким чином.
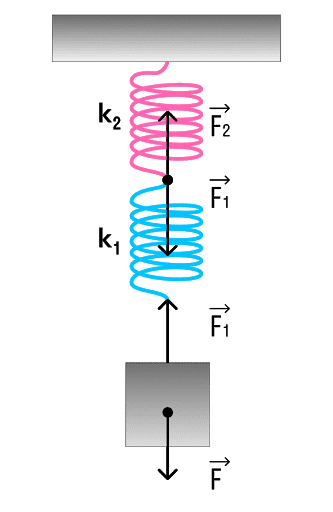
Послідовне з’єднання системи пружин
Послідовне з’єднання характерне наявністю однієї точки з’єднання пружин.
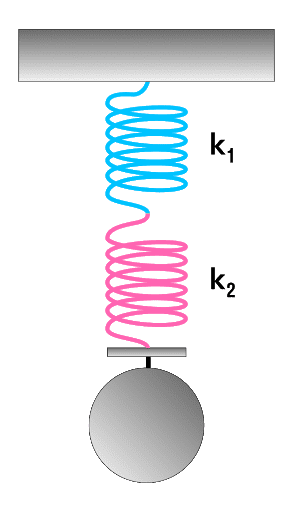
При послідовному з’єднанні загальна жорсткість системи зменшується. Формула для розрахунку коефіцієнта пружності матиме такий вигляд:
Коефіцієнт жорсткості при послідовному з’єднанні пружин \frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}+\dots+\frac{1}{k_i}k — загальна жорсткість системи [Н/м] k1, k2, …, ki — окремі жорсткості кожного елемента [Н/м]< /p> i — загальна кількість усіх пружин, задіяних у системі [-] |
Паралельне з’єднання системи пружин
Послідовне з’єднання характерне наявністю двох точок з’єднання пружин.
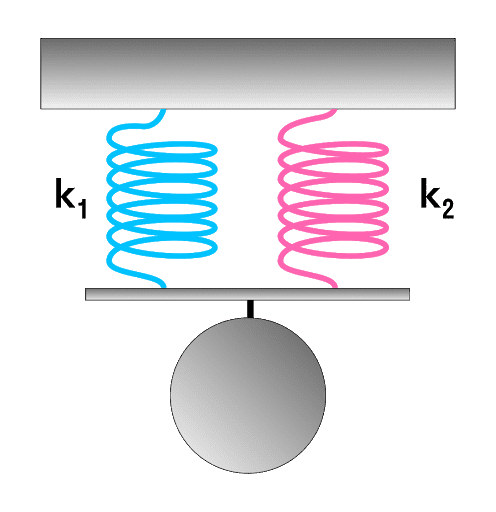
У разі коли пружини з’єднані паралельно величина загального коефіцієнта жорсткості системи буде збільшуватися. Формула для розрахунку виглядатиме так:
| Коефіцієнт жорсткості при паралельному з’єднанні пружин k — загальна жорсткість системи [Н/м] k1, k2, …, k i — окремі жорсткості кожного елемента [Н/м] i — загальна кількість усіх пружин, задіяних у системі [-] |
Завдання
Яка жорсткість системи з двох пружин, жорсткості яких k1 = 100 Н/м, k2 = 200 Н/м, сполучених: а) паралельно; б) послідовно?
Рішення:
а) Розглянемо паралельне з’єднання пружин.
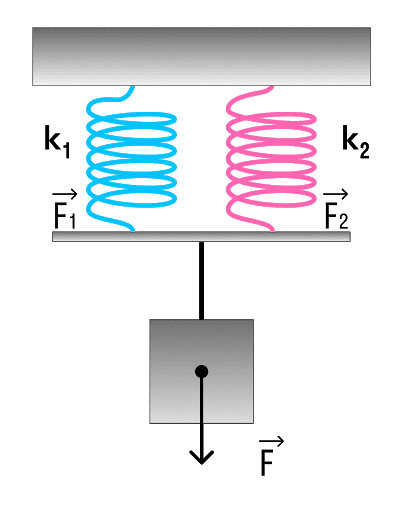
При паралельному з’єднанні пружин загальна жорсткість
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Розглянемо послідовне з’єднання пружин.
При послідовному з’єднанні загальна жорсткість двох пружин
\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}+\dots+\frac{1}{k_i}\frac{1}{k}=\frac{1}{100}+\frac{1}{200}=0,01+0,005=0,015=\frac{15}{1000}k=\frac{1000}{15}=\frac{200}{3}\simeq66,7 Н/мДуже-дуже важливо! Не забудь під час розрахунку жорсткості при послідовному з’єднанні в кінці перевернути дріб.
Графік залежності сили пружності від жорсткості
Закон Гука можна подати у вигляді графіка. Це графік залежності сили пружності від зміни довжини, і по ньому дуже зручно можна розрахувати коефіцієнт жорсткості. Давай розглянемо на прикладі задач.
Завдання 1
Визначте за графіком коефіцієнт твердості тіла.
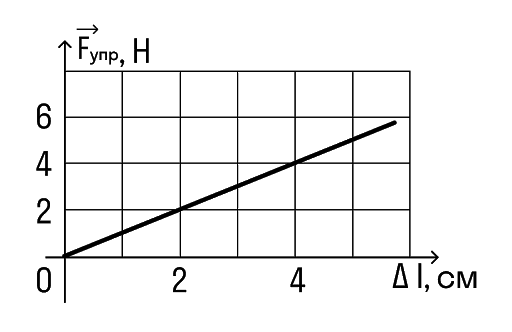
Рішення:
З Закону Гука висловимо коефіцієнт жорсткості тіла:
F = kx
k=F/x
Знімемо значення із графіка. Важливо вибрати одну точку на графіку та записати для неї значення обох величин.
Наприклад, візьмемо ось цю точку.
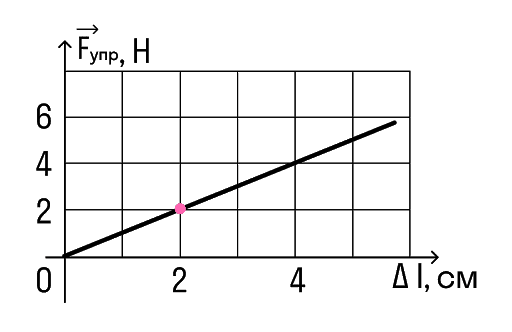
У ній подовження дорівнює 2 см, а сила пружності 2 Н.
Перекладемо сантиметри в метри:
2 см = 0,02 м
І підставимо у формулу:
k=\frac{F}{x}=\frac{2}{0,02}=100 Н /мВідповідь: жорсткість пружини дорівнює 100 Н/м
Завдання 2
На малюнку представлені графіки залежності подовження від модуля прикладеної сили для сталевої (1) та мідної (2) дротів рівної довжини та діаметра. Порівняти жорсткості дротів.
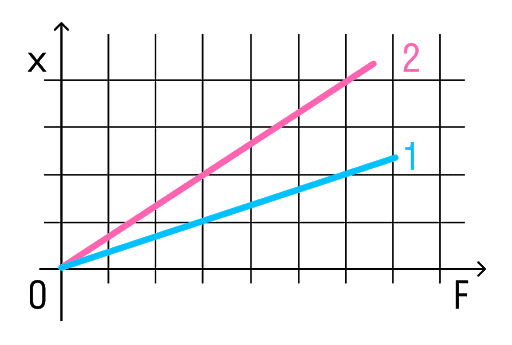
Рішення:
Візьмемо точки на графіках, у яких буде однакова сила, але різне подовження.
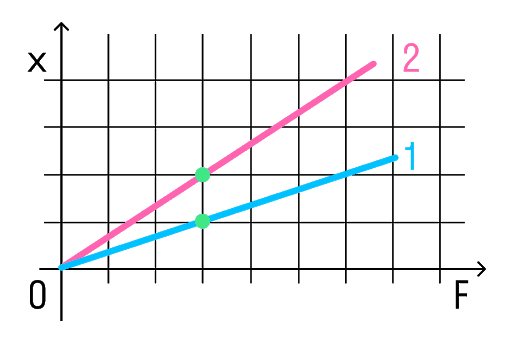
Ми бачимо, що при однаковій силі подовження 2 дроту (мідного) більше, ніж 1 (сталевий). Якщо висловити із Закону Гука жорсткість, то можна побачити, що вона обернено пропорційна подовженню.
k=\frac{F}{x}Значить жорсткість сталевого дроту більше.
Відповідь: жорсткість сталевого дроту більше мідного.