Сучасний світ неможливий без гармонійних коливань – будь-яка електромагнітна хвиля їх поширює. Не було б телефонів, інтернету та інших електронних засобів. Що таке гармонійні коливання — у цій статті.
Механічні коливання
Механічні коливання — це фізичні процеси, які точно або приблизно повторюються через однакові інтервали часу.
Коливання поділяються на два види: вільні та вимушені.
Вільні коливання
Це коливання, які відбуваються під дією внутрішніх сил у коливальній системі.
Вони завжди загасають, тому що весь запас енергії, повідомлений на початку, наприкінці йде на виконання роботи з подолання сил тертя і опору середовища (у цьому випадку механічна енергія переходить у внутрішню). Через це вільні коливання майже не мають практичного застосування.
Вимушені коливання
А вимушені коливання заповнюють запас енергії зовнішнім впливом. Якщо це відбувається кожен період, то коливання взагалі загасати не будуть.
Вимушені коливання— це коливання, які відбуваються під дією зовнішньої сили, що періодично змінюється.
Частота, з якою ця сила впливає, дорівнює частоті, з якою система коливатиметься.
Наприклад, гойдалки. Якщо вас хтось на них качатиме, щоразу даючи поштовх, коли ви приходите в одну й ту саму точку — таке коливання буде вважатися вимушеним.
Це коливання все ще вважатиметься вимушеним, якщо вас будуть розгойдувати зі становища рівноваги. Просто в даному випадку амплітуда (про яку йтиметься трохи нижче) буде збільшуватися з кожним коливанням.
Автоколивання
Іноді вимушеному коливанню не потрібно зовнішнього впливу, щоб статися. Бувають такі системи, в яких ця зовнішня дія виникає саме через здатність регулювати надходження енергії від постійного джерела.
Автоколивальна система має три важливі складові:
- сама коливальна система
- джерело енергії
- пристрій зворотного зв’язку, що забезпечує зв’язок між джерелом і системою.
Годинник з зозулею – приклад автоколивальної системи. Гиря на ниточці (ланцюжку) прагне обертати зубчасте колесо (храповик). При коливаннях маятника анкер чіпляє за зубець і обертання припиняється.
Але в результаті маятник отримує поштовх, що компенсує втрати енергії через тертя. Потенційна енергія гирі, яка поступово опускається, витрачається на підтримку невгамовних коливань.

Характеристики коливань
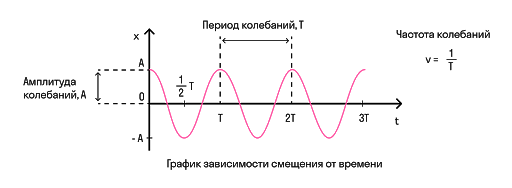
Щоб перейти до гармонічних коливаннь, нам потрібно описати величини, які допоможуть нам ці коливання охарактеризувати. Будь-який коливальний рух можна описати величинами: період, частота, амплітуда, фаза коливань.
Період – це час одного повного коливання. Вимірюється в секундах і позначається буквою T.
| Формула періоду коливань T =t/N T — період [с] t — час [с] N — кількість коливань [—] |
Також є величина, зворотна періоду – частота. Вона показує, скільки коливань здійснює система в одиницю часу.
| Формула частоти ν = N/t = 1/T ν — частота [Гц] t — час [с] T — період [с] N — кількість коливань [—] |
Амплітуда — це максимальне відхилення від положення рівноваги. Вимірюється в метрах і позначається або літерою A, або xmax.
Вона використовується в рівнянні гармонійних коливань:
Гармонічні коливання
Найпростіший вид коливального процесу – прості гармонічні коливання, які описують рівнянням:
| Рівняння гармонійних коливань x = xmaxcos(2πνt) x — координата в момент часу t [м] x max — амплітуда [м] ν — частота [Гц] t — час [с] π = 3 ,14 |
(2πνt) у цьому рівнянні – це фаза. Її позначають грецькою буквою φ
| Фаза коливань φ = 2πνt φ – фаза [рад] ν – частота [Гц] t – момент часу [с] π = 3,14 |
Фаза коливань – це фізична величина, яка показує відхилення точки від положення рівноваги. Погляньте на малюнок, на ньому зображені однакові фази:
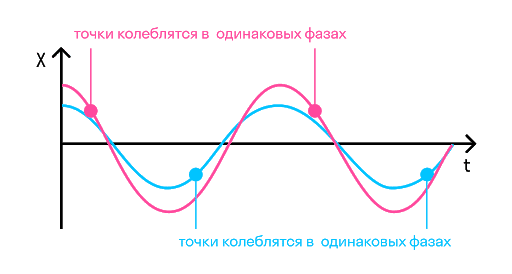
Наприклад, у тих же годинниках з зозулею маятник здійснює коливання. Він хитається зліва направо і приходить у праву точку. У тій же фазі він перебуватиме, коли прийде в ту саму точку, йдучи праворуч наліво. Якщо ми візьмемо крапку на сантиметр лівіше за саму праву, то йдучи в неї не зліва направо, а праворуч наліво, ми отримаємо вже іншу фазу.
На малюнку нижче показано положення тіла через однакові проміжки часу при гармонійних коливаннях. Таку картину можна отримати при освітленні тіла, що коливається, короткими періодичними спалахами світла (стробоскопічне освітлення). Стрілки зображають вектори швидкості тіла в різні моменти часу.
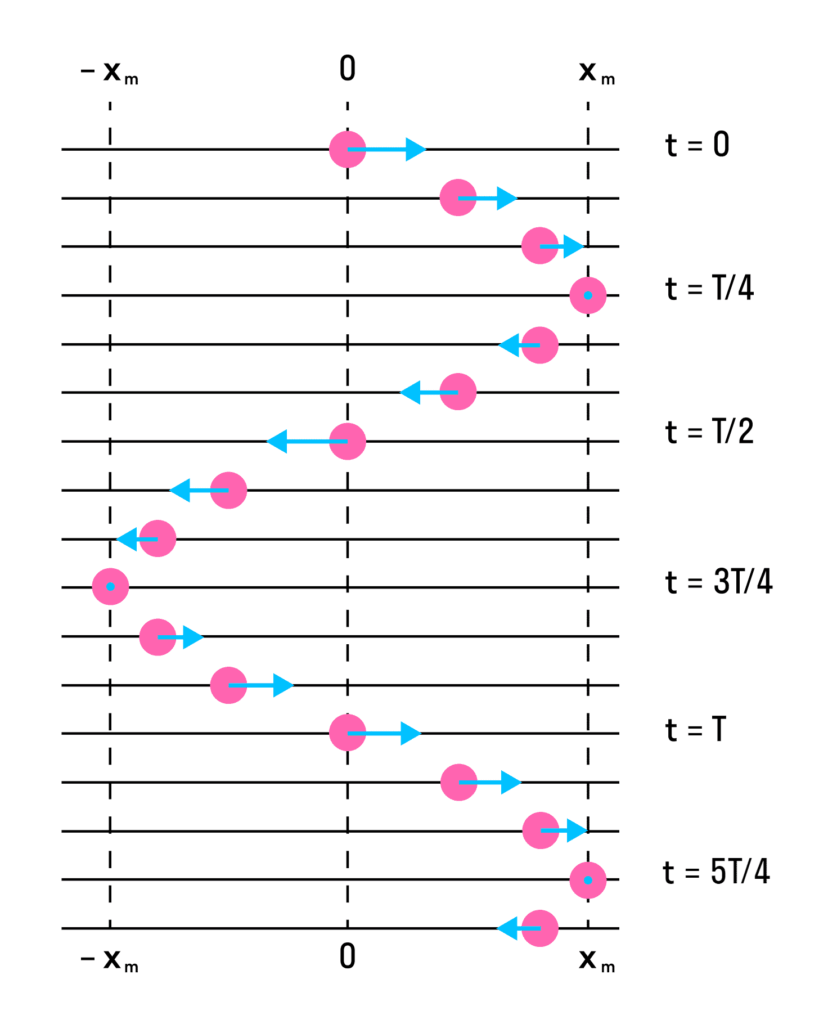
Якщо змінити період, початкову фазу або амплітуду коливання, графіки також зміняться.
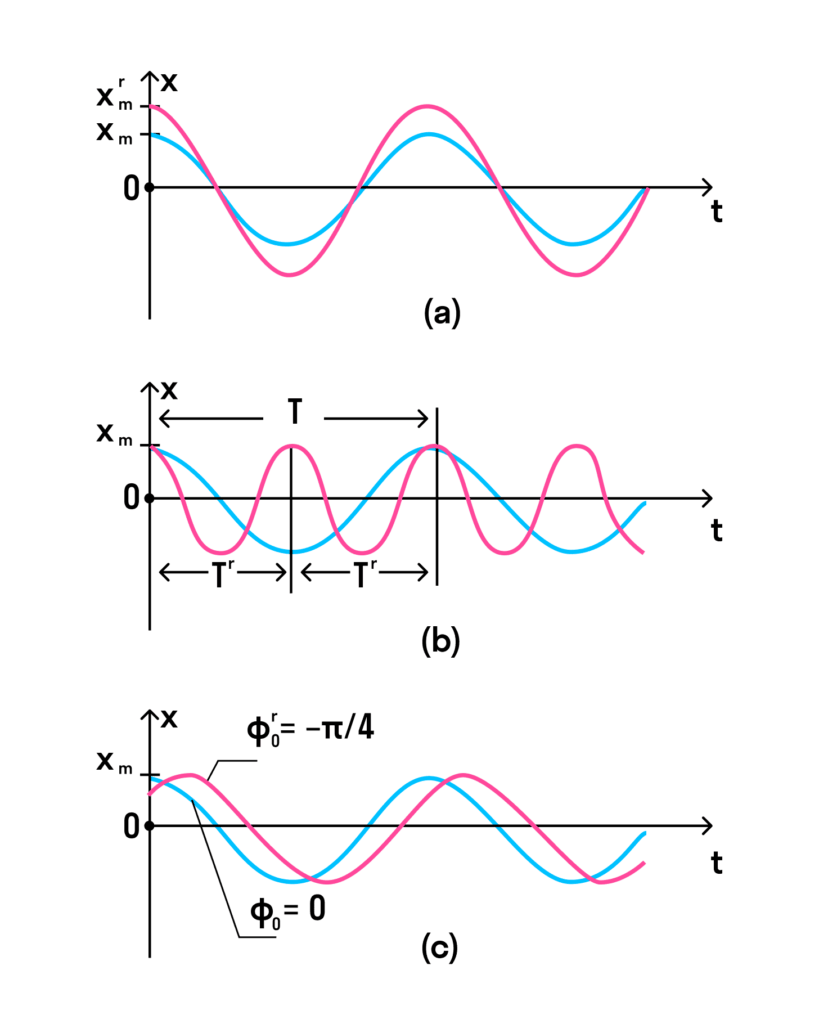
На малюнку нижче у всіх трьох випадках для синіх кривих початкова фаза дорівнює нулю, а в останньому (с) — червона крива має меншу початкову фазу.
- У першому випадку (а) червона крива описує коливання, у якого амплітуда більше коливання, описаного синьою лінією.
- У другому випадку (b) червона крива відрізняється від синьою лише значенням періоду — у червоного періоду вдвічі менше.
Математичний маятник
Математичний маятник – чудовий приклад гармонійних коливань. Якщо ми підвісимо кульку на нитці, то це ще не буде математичним маятником — поки він тільки фізичний.
Математичним цей маятник стане, якщо розміри кульки набагато менші за довжину нитки (тоді цими розмірами можна знехтувати і розглядати кульку як матеріальну точку), розтягнення нитки дуже малий, а маса нитки набагато менше маси кульки.
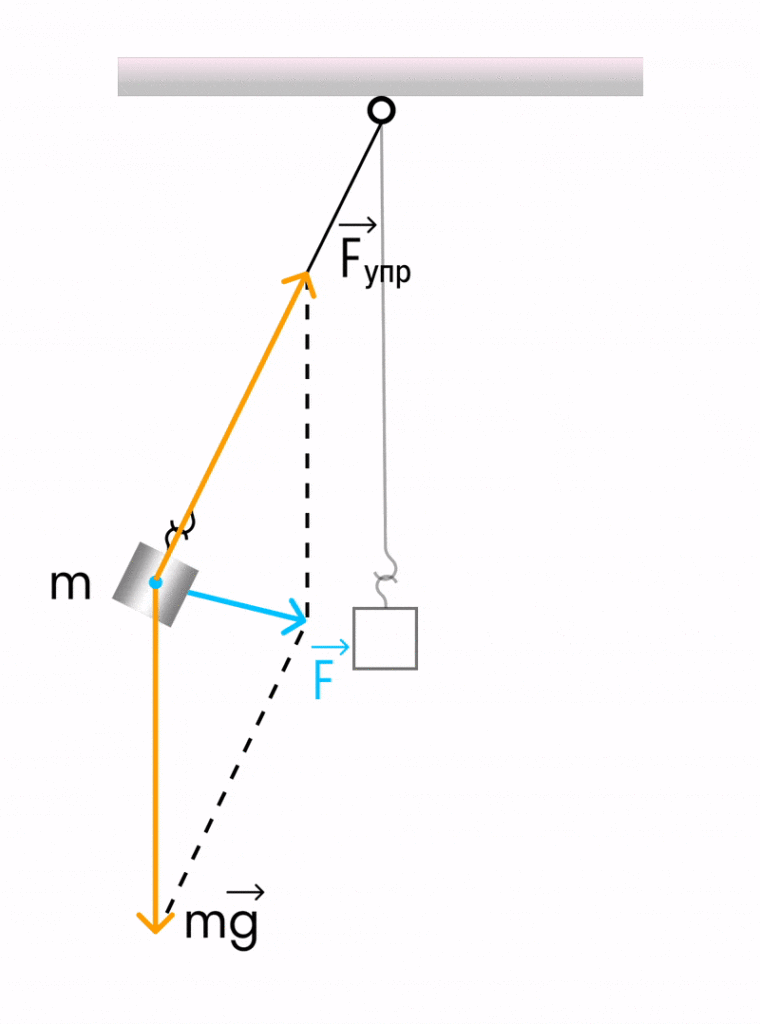
Математичним маятником називається система, яка складається з матеріальної точки масою m та невагомої нерозтяжної нитки довжиною l, на якій матеріальна точка підвішена, і яка знаходиться в полі сили тяжіння (або інших сил).
Період малих коливань математичного маятника у полі сили тяжіння Землі визначається за формулою:
Формула періоду коливання математичного маятника 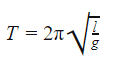 T — період [с] l — довжина нитки [м] g — прискорення вільного падіння [м/с2] На планеті Земля g = 9,8 м/с2 π = 3,14 |
Пружинний маятник
Пружинний маятник — це вантаж, прикріплений до пружини, масою якої можна знехтувати.
У пружинному маятнику коливання відбуваються під впливом сили пружності.
Поки пружина не деформована, сила пружності на тіло не діє.
Формула періоду коливання пружинного маятника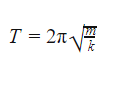 T — період [с] m — маса маятника [кг] k — жорсткість пружини [Н/м] π = 3,14 |
Закон збереження енергії для гармонійних коливань
Фізика — така кльова наука, в якій нічого не зникає безслідно і не з’являється звідки. Цю особливість описує закон збереження енергії.
Розглянемо його на прикладі математичного маятника.
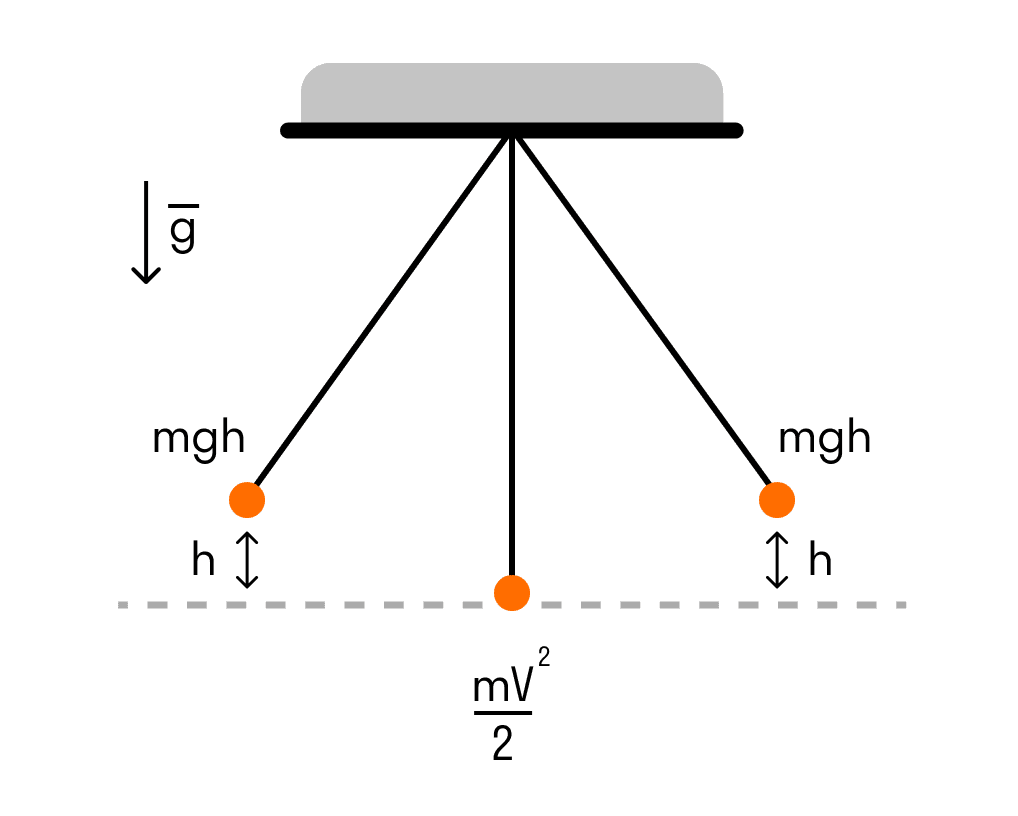
- Коли маятник відхиляють на висоту h, його потенційна енергія максимальна.
- Коли маятник опускається, потенційна енергія перетворюється на кінетичну. Причому у нижній точці, де потенційна енергія дорівнює нулю, кінетична енергія максимальна і дорівнює потенційній енергії у верхній точці. Швидкість вантажу в цій точці максимальна.





