Гравітація схожа на любов – тіла притягуються з рівними за модулем силами, які зменшуються зі збільшенням відстані. Щоправда, сили ще й збільшуються за рахунок збільшення маси, але вдамо, що однаково схоже.
Гравітаційна взаємодія
Земля це великий магніт. Причому насправді магніт, із справжнім магнітним полем. Але зараз мова піде про інше явище — явище тяжіння тіл до Землі, від котика, що стрибає з дерева, до астероїда, що летить. Називається це явище гравітацією.
Візьмемо два тіла — одне з великою масою, інше з маленькою. Натягнемо гігантське полотно тканини і покладемо на нього тіло з більшою масою. Після чого покладемо туди тіло з меншою масою. Ми спостерігатимемо приблизно таку картину:
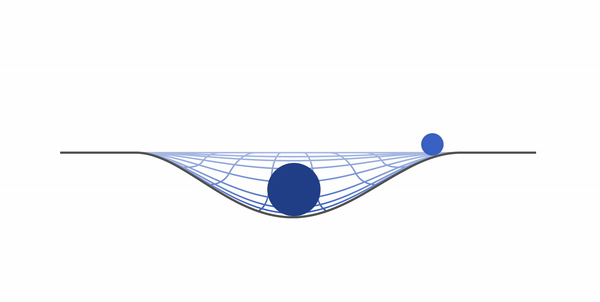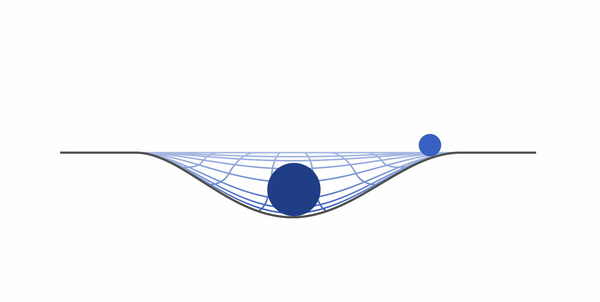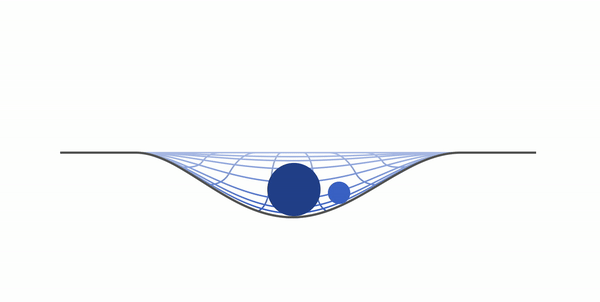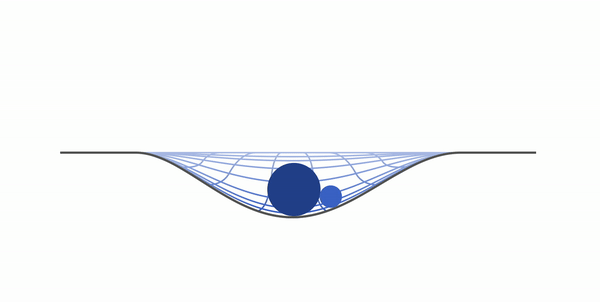
Маленьке тіло почне притягуватися до того, що більше — це гравітація. По суті, Земля — це велика кулька, а решта предметів — маленька (навіть якщо це зовсім не кульки).
Гравітаційна взаємодія є універсальною. Воно справедливе всім видів матерії. Гравітація проявляється тільки в тяжінні – відштовхування тіл гравітація не передбачає.
З усіх фундаментальних взаємодій гравітаційне найслабше. Хоча гравітація діє між усіма елементарними частинками, вона настільки слабка, що її прийнято не враховувати. Справа в тому, що гравітаційна взаємодія залежить від маси об’єкта, а у частинок вона вкрай мала. Цю залежність вперше сформулював Ісаак Ньютон.
Закон всесвітнього тяжіння
У 1682 році Ісаак Ньютон відкрив закон всесвітнього тяжіння. Він звучить так: всі тіла притягуються одне до одного, сила всесвітнього тяжіння прямо пропорційна добутку мас тіл і обернено пропорційна квадрату відстані між ними.
Формула сили тяжіння відповідно до цього закону виглядає так:
| Закон всесвітнього тяжіння
F = G \frac{Mm}{R^2}F — сила тяжіння [Н] M – маса першого тіла (часто планети) [кг] m – маса другого тіла [кг] R — відстань між тілами [м] G — гравітаційна постійна G = 6,67 · 10−11м3 · кг−1 · c−2 |
Коли ми встаємо на терези, стрілка відхиляється. Це відбувається тому, що маса Землі дуже велика, і сила тяжіння буквально притискає нас до поверхні. На легшому Місяці людина важить менше приблизно у шість разів.
Закон всесвітнього тяжіння використовують, щоб обчислити сили взаємодії між тілами будь-якої форми, якщо розміри тіл значно менші за відстань між ними.
Якщо ми візьмемо дві кулі, то для них можна використати цей закон незалежно від відстані між ними. За відстань R між тілами в цьому випадку приймається відстань між центрами куль.
Задача раз
Дві планети з однаковими масами звертаються по кругових орбітах навколо зірки. У першій з них радіус орбіти вдвічі більший, ніж у другої. Яким є відношення сил тяжіння першої та другої планети до зірки?
Рішення
За законом всесвітнього тяжіння сила тяжіння планети до зірки обернено пропорційна квадрату радіуса орбіти. Таким чином, в силу рівності мас відношення сил тяжіння до зірки першої та другої планет обернено пропорційно відношенню квадратів радіусів орбіт:
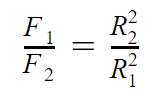
За умовою, у першої планети радіус орбіти вдвічі більший, ніж у другої, тобто R1 = 2R2.
Це означає, що:
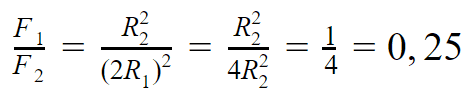
Відповідь: відношення сил тяжіння першої та другої планет до зірки дорівнює 0,25.
Завдання два
У поверхні Місяця на космонавта діє сила тяжіння 144 Н. Яка сила тяжіння діє з боку Місяця на того ж космонавта в космічному кораблі, що рухається круговою орбітою навколо Місяця на відстані трьох місячних радіусів від її центру?
Рішення
За законом всесвітнього тяжіння сила тяжіння космонавта з боку Місяця обернено пропорційна квадрату відстані між ним і центром Місяця. У поверхні Місяця це відстань збігається з радіусом супутника. На космічному кораблі, за умовою, воно втричі більше. Таким чином, сила тяжіння з боку Місяця, що діє на космонавта на космічному кораблі, у 9 разів менша, ніж у поверхні Місяця, тобто:
144 : 9 = 16 Н
Відповідь: на відстані трьох місячних радіусів від центру сила тяжіння космонавта дорівнюватиме 16 Н.
Важливий нюанс! Правильно говорити не «на тіло діє сила тяжіння», а «Земля притягує тіло із силою тяжіння».
Прискорення вільного падіння
Щоб математично правильно і красиво дійти прискорення вільного падіння, нам необхідно спочатку ввести поняття сили тяжіння.
Сила тяжіння — це сила, з якою Земля притягує всі тіла.
Сила тяжіння F = mg F — сила тяжіння [Н] m — маса тіла [кг] g – прискорення вільного падіння [м/с2] На планеті Земля g = 9,8 м/с2, але докладніше про це трохи пізніше . ? |
На перший погляд, сила тяжіння дуже схожа на вагу тіла. Справді, у стані спокою лежить на поверхні Землі формули сили тяжкості і ваги ідентичні. Вага тіла в стані спокою чисельно дорівнює масі тіла, помноженої на прискорення вільного падіння, різниця полягає лише в точці докладання сили.
Сила тяжіння — це сила, з якою Земля діє на тіло, а вага — сила якою тіло діє на опору. Це означає, що у них будуть різні точки докладання: у сили тяжіння до центру мас тіла, а у ваги — до опори.
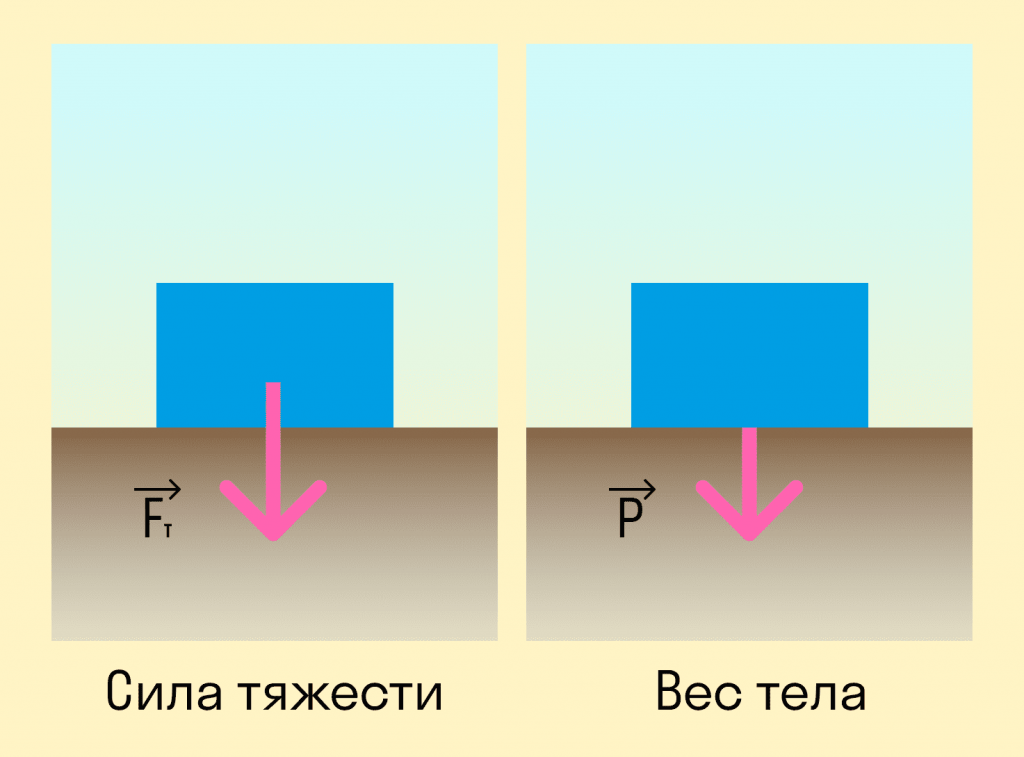
Також важливо розуміти, що сила тяжіння залежить виключно від маси та планети, на якій тіло знаходиться. А вага залежить ще й від прискорення, з яким рухається тіло чи опора.
Наприклад, у ліфті вага залежить від того, куди та з яким прискоренням рухаються його пасажири. А силі тяжіння все одно, куди і що рухається — вона не залежить від зовнішніх факторів.
На другий погляд, сила тяжіння дуже схожа на силу притяжіння. В обох випадках ми маємо справу з притяжінням — отже, можемо сказати, що це одне й те саме. Практично.
Ми можемо сказати, що це те саме, якщо йдеться про Землю і якийсь предмет, який до неї притягується. Тоді ми можемо навіть прирівняти ці сили та висловити формулу для прискорення вільного падіння:
F = mg
F = G \frac{Mm}{R^2}Прирівнюємо праві частини:
mg = G \frac{Mm}{R^2}Ділімо на масу тіла ліву та праву частини:
g = G \frac{M}{R^2}Це буде формула прискорення вільного падіння. Прискорення вільного падіння для кожної планети є унікальним.
| Закон всесвітнього тяжіння
g = G \frac{M}{R^2}g — прискорення вільного падіння [м/с2] M — маса планети [кг]< /p> R — відстань між тілами [м] G — гравітаційна постійна G = 6, 67 · 10−11м3 · кг−1 · с−2 |
Прискорення вільного падіння характеризує те, як швидко збільшується швидкість тіла при вільному падінні.
Вільне падіння — це прискорений рух тіла в безповітряному просторі, при якому на тіло діє лише сила тяжіння.
Але хіба це ще не залежить від маси предмета?
Ні, не залежить. Насправді, всі тіла падають однаково незалежно від маси. Якщо ми візьмемо перо і м’яч, то перо, звичайно, падатиме повільніше, але не через прискорення вільного падіння. Просто через невелику масу пера опір повітря має на нього більший вплив, ніж на м’яч. А ось якби ми помістили перо і м’яч у вакуум, вони б упали одночасно.
Третій закон Ньютона
Третій закон Ньютона узагальнює величезну кількість дослідів, які показують, що сили — результат взаємодії тіл.
Він звучить так: тіла діють один на одного з силами, рівними за модулем і протилежними у напрямку.
Якщо простіше — сила дії дорівнює силі протидії.
Якщо вам раптом доведеться пояснювати фізику на подвір’ї, то можна сказати й так: на кожну силу знайдеться інша сила. ?
| Третій закон Ньютона
\vec{F_1} = - \vec{F_2}F 1 – сила, з якою перше тіло діє на друге [Н] F2 – сила , З якою друге тіло діє на перше [Н] |
Так ось, для сили тяжіння третій закон Ньютона теж справедливий. З якою силою Земля притягує тіло, з тією ж силою тіло притягує Землю.
Завдання для практики
Земля притягує до себе підкинутий м’яч із силою 5 Н. З якою силою цей м’яч притягує до себе Землю?
Рішення
Згідно з третім законом Ньютона, сила, з якою Земля притягує м’яч, дорівнює силі, з якою м’яч притягує Землю.
Відповідь: м’яч притягує Землю з силою 5 Н.
Спочатку це здається дивним, тому що ми асоціюємо силу з переміщенням: мовляв, якщо сила така сама, то на ту саму відстань посунеться Земля. Формально це так, але у м’яча маса набагато менша, ніж у Землі. І Земля зміщується на таку крихітну відстань, притягуючись до м’яча, що ми його не бачимо, на відміну від падіння м’яча.
Якщо кожен кинутий м’яч зміщує Землю на якусь відстань, нехай навіть крихітну, виникає питання. як вона ще не злетіла з орбіти через всі ці зсуви. Але тут як у перетягуванні каната: якщо його тягнуть дві рівні за силою команди, канат нікуди не зрушить. Так само і з нашою планетою.



