«Сиджу, нікого не чіпаю, вирішую завдання з ЗНО, а тут у рішенні астрономічного 24-го якісь закони Кеплера. Нічого не зрозуміло, але дуже цікаво», — так думають багато одинадцятикласників, які здають фізику. Розповідаємо, як зрозуміти ці закони та використовувати у вирішенні завдань.
Форма Землі
Зараз нам складно уявити, що раніше люди вірили, що Земля плоска. У греків, наприклад, площина просто ширяла в повітрі і була оточена льодовиками. А в Індії вірили, що планета лежать на трьох слонах, які стоять на черепаху. Втім, дехто досі так думає. Доказів того, що наша планета насправді не плоска — багато, але ось вам парочка, щоб можна було підтримати світську бесіду.
Зміна дня та ночі
За уявленнями прихильників плоскої Землі, день і ніч змінюються, тому що Місяць та Сонце обертаються над Землею — ось якось так:
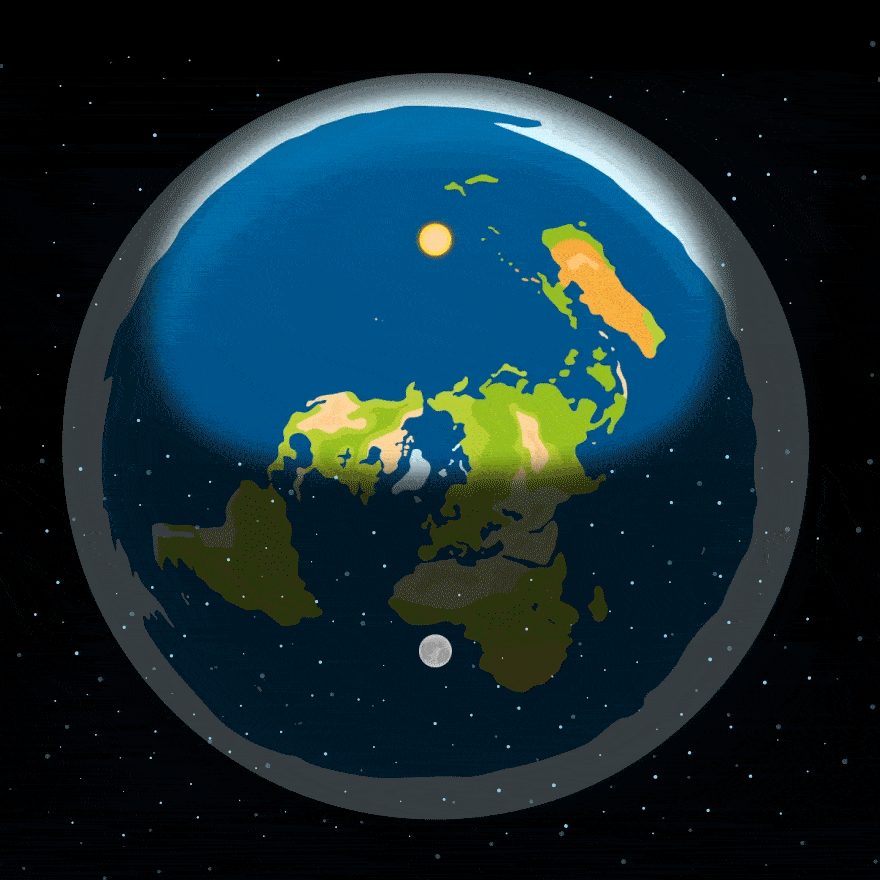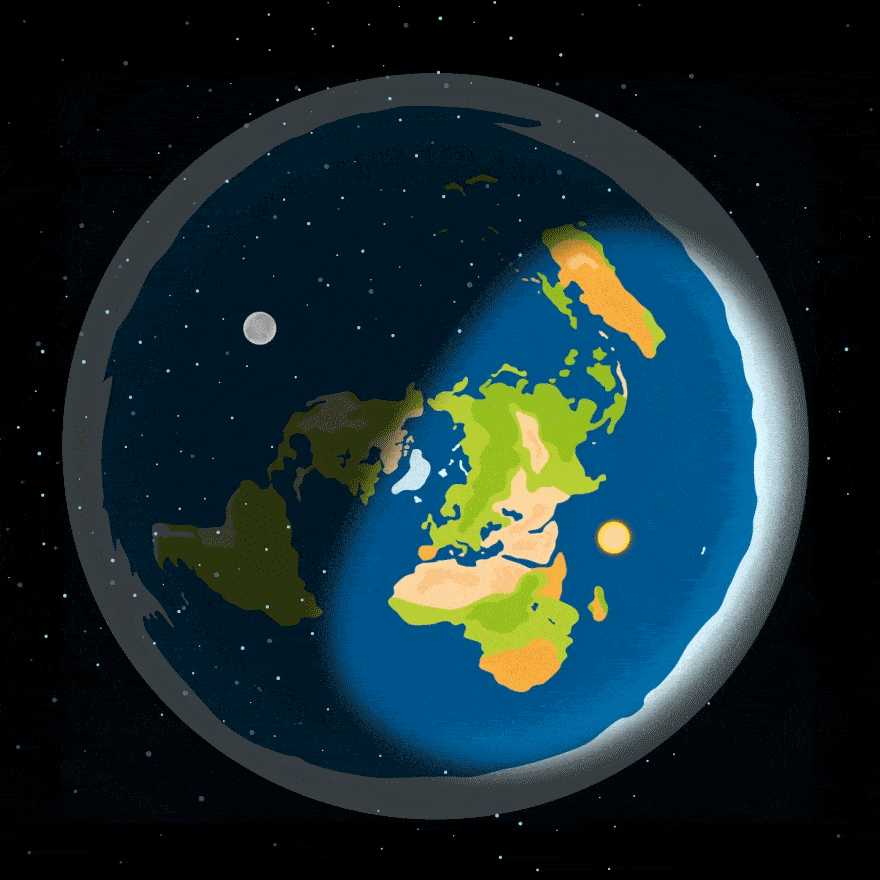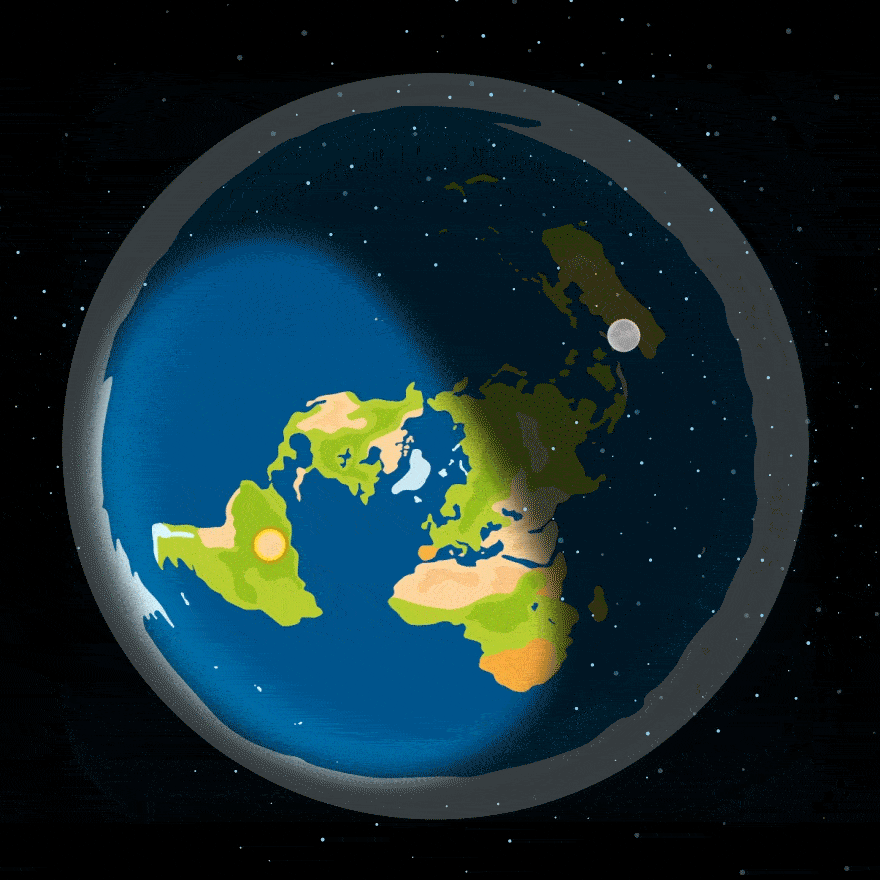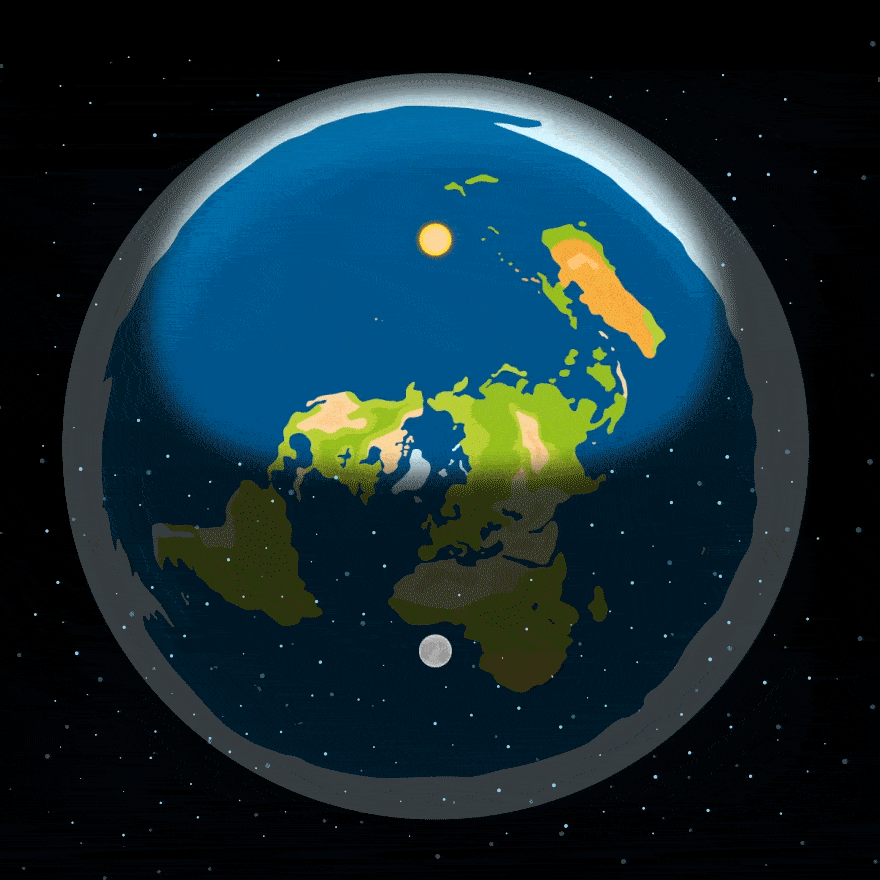
Але – упс! — ця модель викликає цілу низку запитань:
- Чому довжина дня і ночі змінюється протягом року? сходу?
- Чому іноді ми можемо побачити Місяць і Сонце одночасно?
- Чому Місяць і Сонце не з’являються щоразу з одного і тієї ж точки?
- Якщо немає гравітаційного тяжіння, чому вони взагалі крутяться?
Місячне затемнення
Якщо Земля плоска, то незрозуміло, як пояснити місячні затемнення. Щоб затемнення сталося, потрібно, щоб Сонце знаходилося з одного боку від диска, а Місяць — з іншого. Тоді ламається концепція дня і ночі, яку ми описали вище, адже день і ніч будуть наступати для всієї Землі одночасно.
Тіні
На плоску Землю світло від Сонця падало б, як світло від ліхтаря. Тобто високі об’єкти у протилежному від Сонця напрямі після заходу сонця залишалися б у тіні.
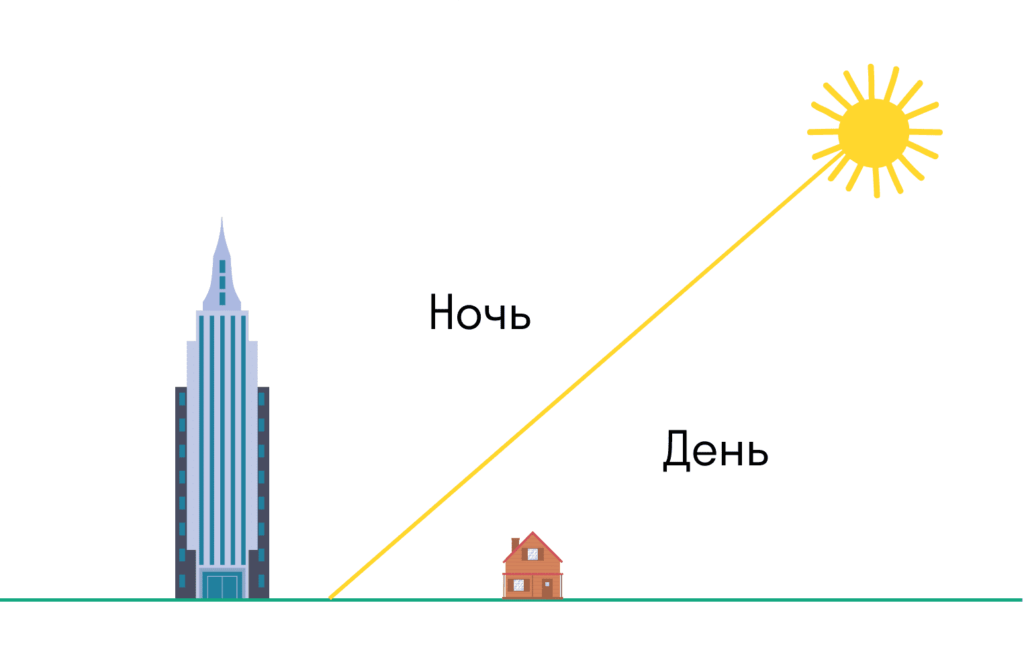
А на кулястій Землі хмарочоси або гори будуть освітлені Сонцем після заходу сонця або перед світанком.
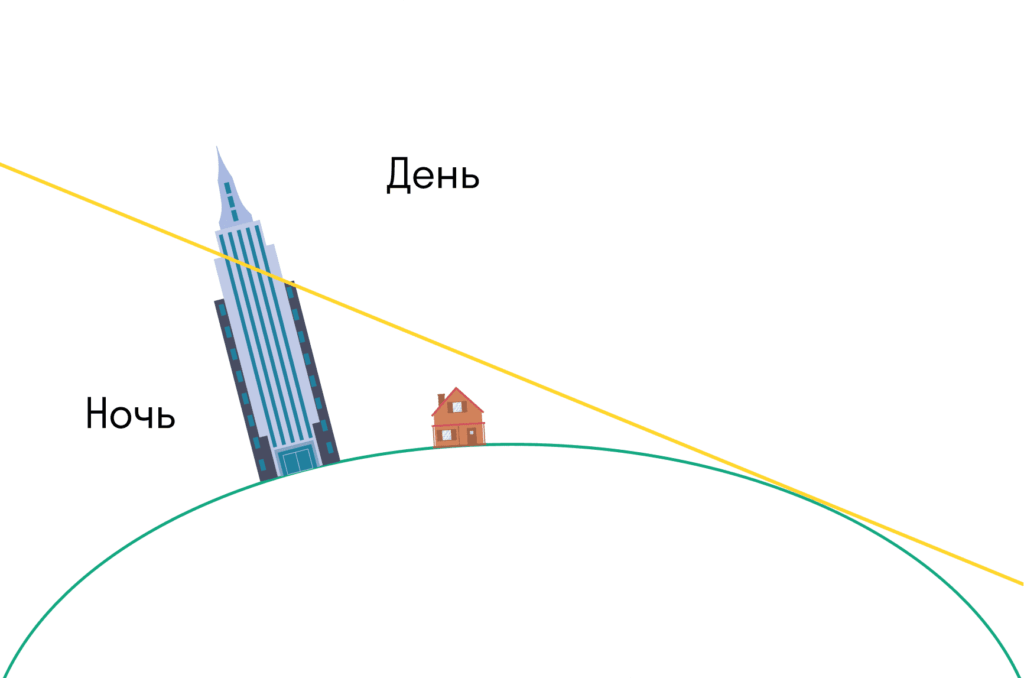
Саме це ви побачите, якщо застанете світанок або захід сонця в горах — або подивіться на фотографії.
Окей, Земля все ж таки не плоска — з цим розібралися. Але й кулею її назвати не можна: Земля має форму еліпсоїда.
Еліпсоід — це така плеската куля, в одному з перерізів у якої еліпс. Саме траєкторією еліпса обертаються всі супутники.
Еліпс
Еліпс — це замкнута пряма на площині, окремий випадок овалу. У еліпса дві осі симетрії – горизонтальна і вертикальна, які складаються з двох півосей.
А ще у еліпса два фокуси – це такі точки, сума відстаней від яких до будь-якої точки P(x, y) є постійною величиною.
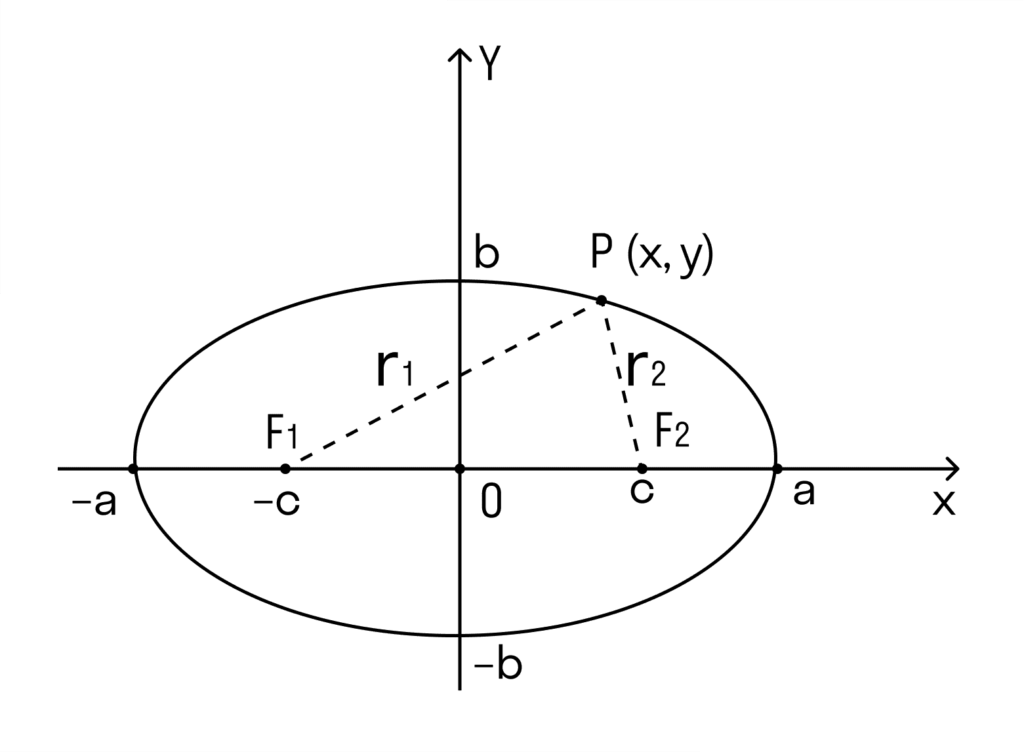
| Еліпс F1 та F2 — фокуси F1 = ( c ; 0) F2 = (-c ; 0) с — половина відстані між F1 та F2 a – велика піввісь b – мала піввісь r1 та r2 — фокальні радіуси |
Тепер ми знаємо всі необхідні поняття, щоб розібратися, у чому полягають закони Кеплера.
Перший закон Кеплера
Кожна планета сонячної системи обертається навколо Сонця по еліпсоїдній орбіті, в одному з фокусів якого знаходиться Сонце.
Сонце знаходиться в одному з фокусів еліпса. Найближча до Сонця точка B траєкторії називається перигелієм, а точка A, найбільш віддалена від Сонця — афелієм.
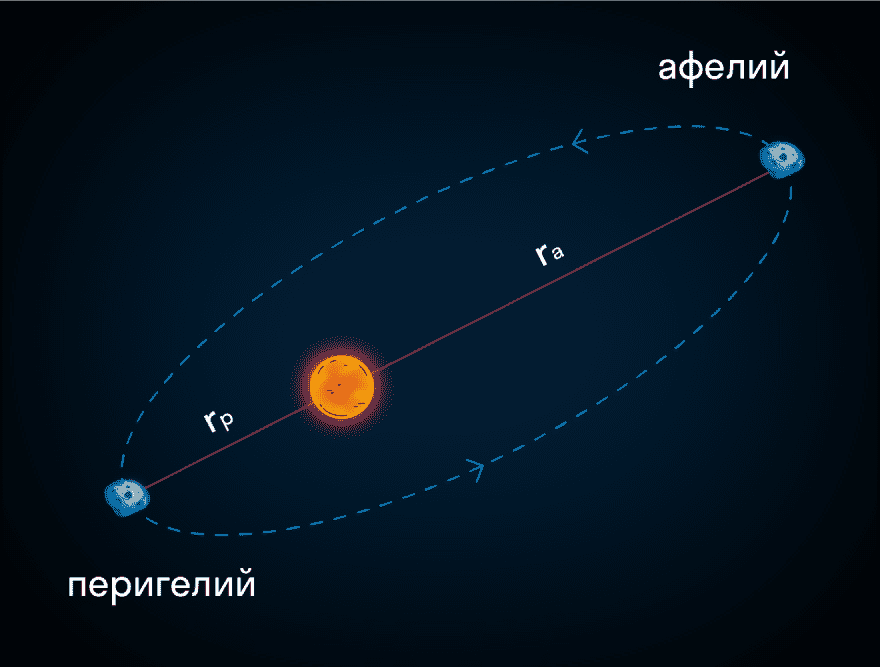
Перший закон Кеплера досить простий, але важливий, тому що свого часу він сильно просунув астрономію. До цього відкриття астрономи вважали, що планети рухаються виключно круговими орбітами. Якщо ж спостереження суперечили цьому переконанню, вчені доповнювали головний круговий рух малими колами, які описували планети навколо точок основної кругової орбіти. Кеплер отримав доступ до величезної бази спостережень Тихо Браге і, вивчивши їх, переступив старі ідеї.
Другий закон Кеплера (закон площ)
Радіус-вектор, що з’єднує планету і Сонце, описує в рівні проміжки часу рівні площі.
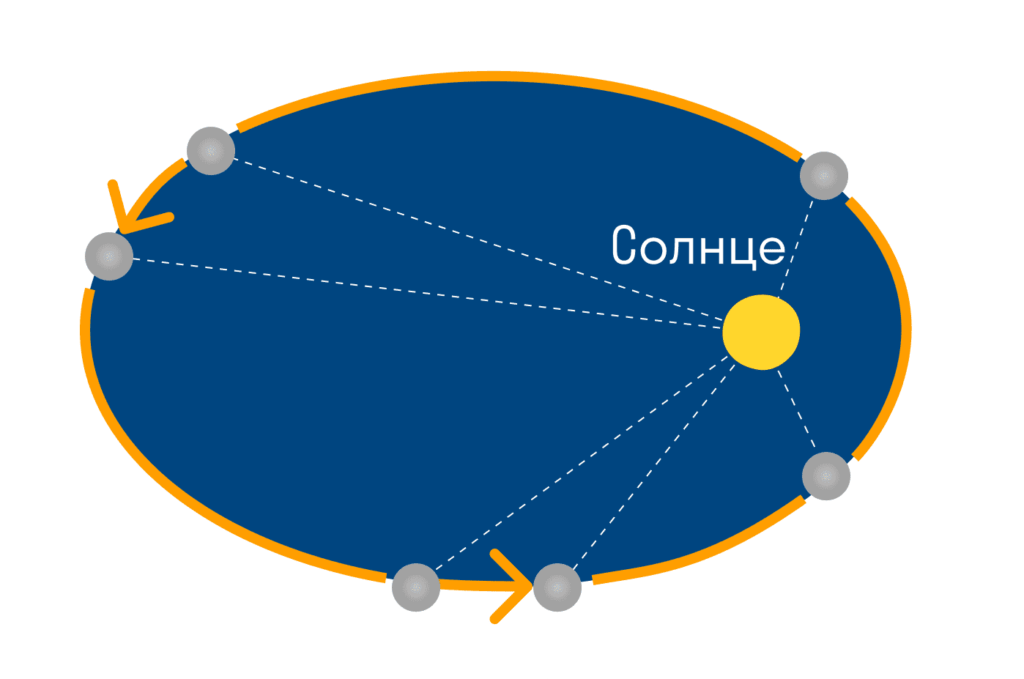
Кожна планета переміщається у площині, що проходить через центр Сонця. За рівні проміжки часу радіус-вектор, що з’єднує Сонце та планету, визначає рівні площі. Таким чином, тіла рухаються навколо Сонця нерівномірно: у перигелії вони мають максимальну швидкість, а в афелії – мінімальну.
На практиці це можна помітити за рухом Землі. Щорічно на початку січня наша планета проходить через перигелій та переміщується швидше. Через це рух Сонця з екліптики (лінії, що показує шлях Сонця по небу) також відбувається швидше, ніж в інший час року. На початку липня Земля рухається через афелій, через що Сонце з екліптики переміщається повільніше. Тому світловий день влітку довший, ніж узимку.
Третій закон Кеплера
Квадрати періодів обігу планет відносяться як куби великих півосей їх орбіт.
Згідно з третім законом Кеплера, між періодом обігу планет навколо Сонця і великими півосями їх орбіт встановлюється зв’язок. Цей закон виконується як для планет, так і для супутників з похибкою менше 1%.
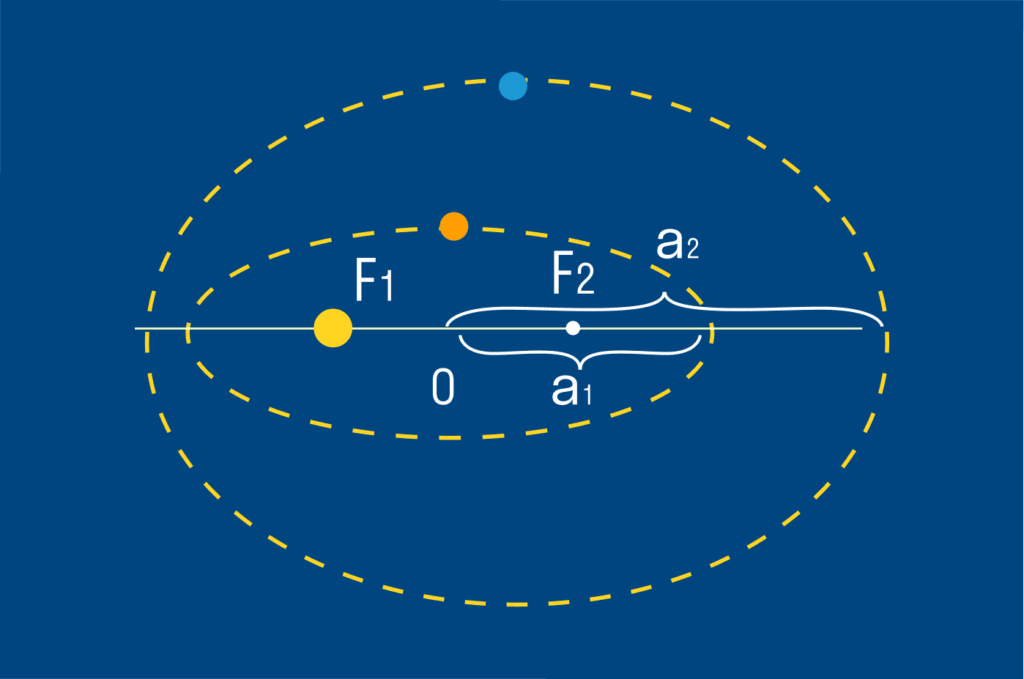
Третій закон Кеплера\frac{T_1^2}{T_2^2}=\frac{a_1^3}{a_2^3}T1 та T2 — періоди обігу двох планет [c] a1 та a2 – великі півосі орбіт планет [м] |
На основі цього закону можна обчислити тривалість року (часу повного обороту навколо Сонця) будь-якої планети якщо відомо її відстань до Сонця в афелії.
Також можна зробити зворотне – розрахувати орбіту, знаючи період звернення.
Закон всесвітнього тяжіння
Закони Кеплера – це результати спостережень та узагальнень. Згодом вони лягли в основу закону всесвітнього тяжіння, який звучить так: всі тіла притягуються один до одного, сила всесвітнього тяжіння прямо пропорційна добутку мас тіл і обернено пропорційна квадрату відстані між ними.
Формула сили тяжіння відповідно до цього закону виглядає так:
Закон всесвітнього тяжіння F = G \frac{Mm}{R^2}F — сила тяжіння [Н] M – маса першого тіла (часто планети) [кг] m – маса другого тіла [кг] R – відстань між тілами [м] G — гравітаційна постійна G = 6,67 · 10−11м 3 · кг−1 · з−2 |
Ньютон був першим дослідником, який дійшов висновку, що між будь-якими тілами в космосі діють гравітаційні сили, і саме вони визначають характер руху цих тіл.
Перша та друга космічні швидкості
Закони Кеплера застосовуються не тільки до руху планет та інших небесних тіл у Сонячній системі, але й до руху штучних супутників Землі та космічних кораблів. І тут центром тяжіння є Земля
У серії книг Дугласа Адамса “Автостопом по Галактиці” говориться, що літати – це просто промахуватися повз Землю. Щоб промахнутися повз Землю та стати її штучним супутником, потрібно досягти першої космічної швидкості 7,9 км/с. Ось як це відбувається:
Штучний супутник Землі — космічний літальний апарат, що обертається навколо Землі геоцентричною орбітою. Щоб у нього це виходило, апарат повинен мати початкову швидкість, яка дорівнює або більше за першу космічну.
Перша космічна швидкістьv_1=\sqrt{gR}v1 – перша космічна швидкість [м/с] |
Є ще друга та третя космічні швидкості. Друга космічна швидкість – це швидкість, яка потрібна, щоб корабель став штучним супутником Сонця, а третя – щоб вилетів за межі сонячної системи.
Друга космічна швидкістьv_2=\sqrt{2gR}v2 – перша космічна швидкість [м/с] |