Момент сили

Попередня стаття Наступна стаття

Можливо, ви ніколи не помічали, але щоразу ви штовхаєте прозорі двері в метро, ставлячи руку не ближче до кріплення, а навпаки ближче до краю. Поняття «Момент сили» пояснить цю інтуїтивну дію.

Сила: що це за величина

У повсякденному житті ми часто зустрічаємо, як будь-яке тіло деформується (змінює форму або розмір), прискорюється або сповільнюється, падає. Загалом чого тільки з різними тілами в реальному житті не відбувається. Причиною будь-якої дії чи взаємодії є сила.

Сила — це фізична векторна величина, є мірою дії тіла на інше тіло.

Вона вимірюється в ньютонах — це одиниця виміру названа на честь Ісаака Ньютона.

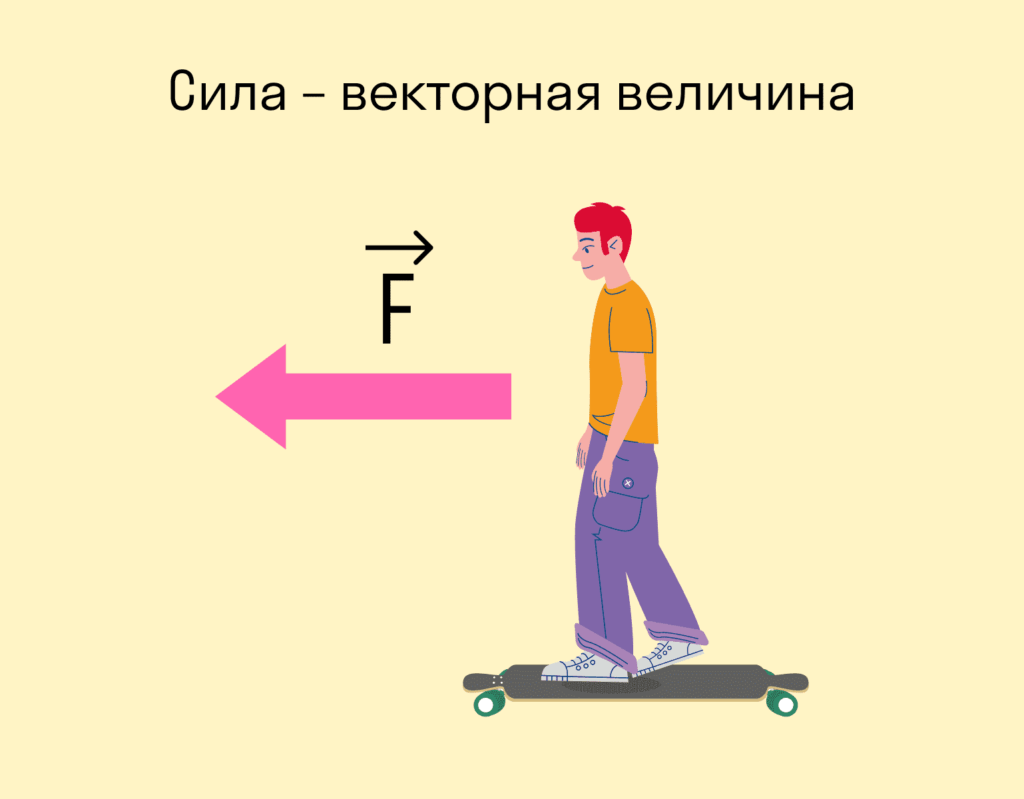
Сила — величина векторні. Це означає, що, крім модуля, вона має напрямок. Від того, куди спрямовано силу, залежить результат.

Ось стоїте ви на лонгборді: можете відштовхнутися праворуч, а можете ліворуч – залежно від того, в який бік відштовхнетеся, результат буде різним. У разі результат виявляється у напрямі руху.

Плече сили

Для початку давайте розберемося, що таке плече сили — воно нам сьогодні стане в нагоді.

Уявіть людину. Цілком звичайного. Якщо він звичайний, у нього точно будуть плечі — без них вийде вже якийсь інопланетянин. Якщо ми прокреслимо пряму вздовж лінії плеча, а потім ще одну – вздовж лінії руки – ми отримаємо дві прямі, що перетинаються. Кут між такими прямими дорівнюватиме 90 градусів, а значить ці лінії перпендикулярні.

Як анатомічне плече перпендикулярне руці, так і у фізиці плече перпендикулярне, тільки вже лінії дії сили.

Тобто перпендикуляр, проведений від точки опори до лінії, вздовж якої діє сила — це плече сили.

Важіль

У кожному дворі є гойдалки, для яких потрібні два гойдаючі (якщо у вашому дворі таких немає, подивіться в сусідньому). Велика дошка ставиться посередині на точку опори. По суті, гойдалки – це важіль.

Важіль — найпростіший механізм, що є балкою, що обертається навколо точки опори.

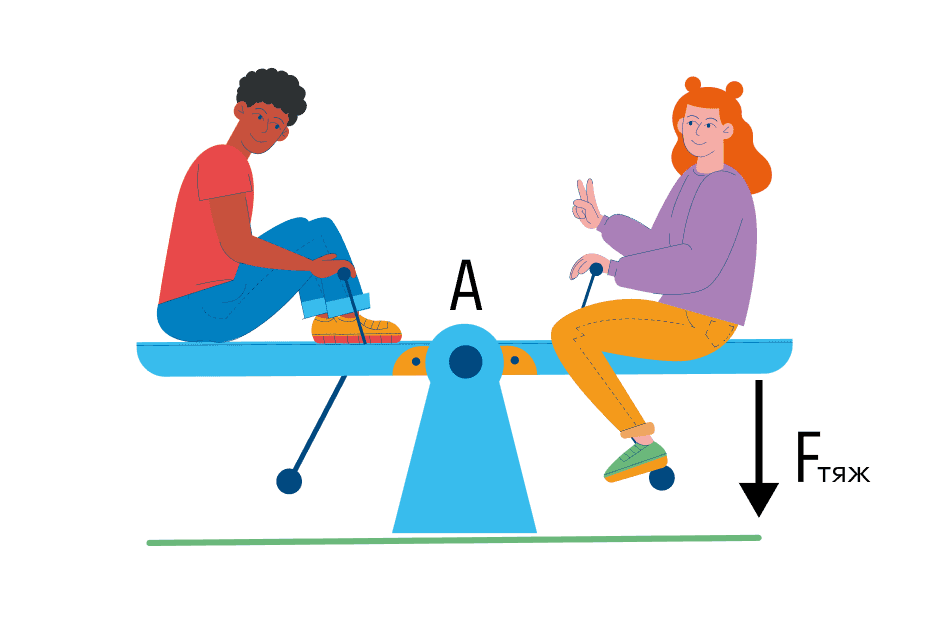
Добре, тепер знайдемо плече цієї конструкції. Візьмемо праву частину гойдалки. На гойдалці діє сила тяжіння правого хитається, проведемо перпендикуляр від лінії дії сили до точки опори. Вийшло, що плече збігається з важелем, хіба що важіль – це вся конструкція, а плече – половина.

Давайте спробуємо опустити гойдалку праворуч, тоді що отримаємо: важіль залишився тим самим по довжині, але ось змістився на деякий кут, а ось плече залишилося на тому ж місці. Якщо напрям дії сили не змінюється , Як і точка опори, то перпендикуляр між ними неможливо змінити.

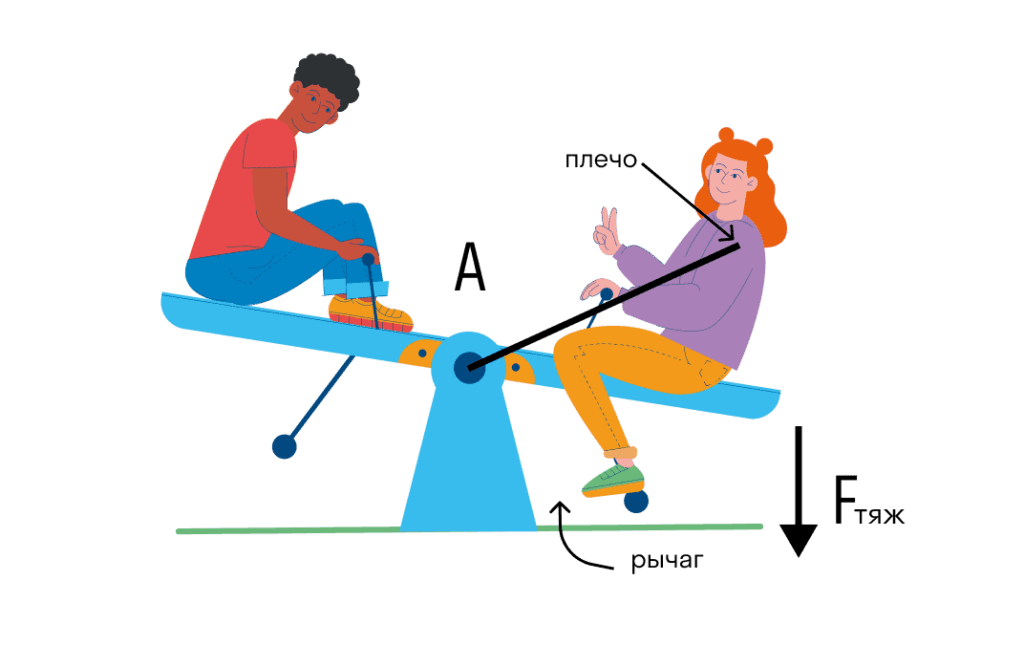
Правило рівноваги важеля
Важіль знаходиться в рівновазі тоді, коли сили, що діють на нього, обернено пропорційні плечам цих сил.

\frac{F_1}{F_2}=\frac{l_2}{l_1}

F₁, F₂ — сили, що діють на важіль
l₁, l₂ — плечі цих сил

При вирішенні завдань різні сили нам зазвичай вистачало просто сил. Сила діє завжди лінійно (ну в найгіршому разі під кутом), тому дуже зручно користуватися законами Ньютона, прирівнювати різні сили. Це працювало з матеріальними точками, але не так просто застосовуватися до тіл, у яких є форма і розмір.

Ось ми приклали силу до краю палиці, але при цьому не можемо сказати, що на іншому її кінці будуть те саме прискорення і та сама сила. І тому ми вводимо таке поняття, як момент сили.

Момент сили — це витвір сили на плече. Для визначення фізичного сенсу можна сказати, що момент – це обертальна дія.

Момент сили
M=Fl
M — момент сили [Н*м]
F — сила [Н]
l — плече [м]

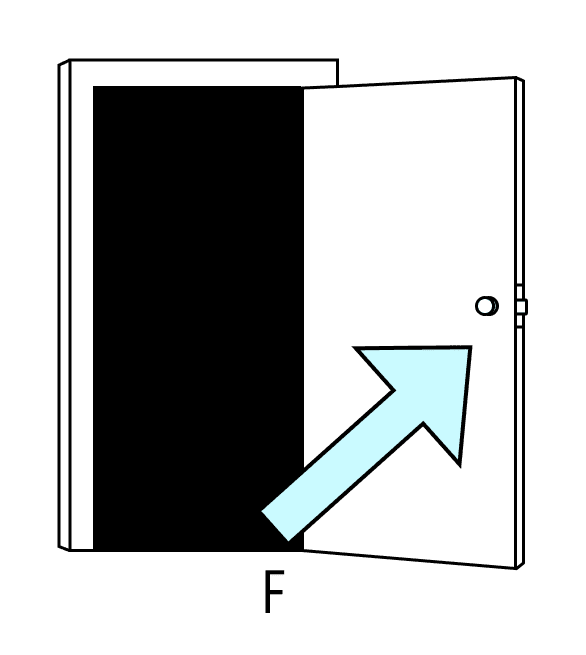
Для прикладу уявіть, що ви забули, як відчиняти двері. Стоїте перед дверима і роздумуєте, як це зробити.

Для початку прикладемо силу до краю дверей — туди, де найдовший важіль. Відкрилися!

А якщо штовхнути двері ближче до кріплення — там, де плече набагато коротше? Для цього доведеться докласти силу більшого значення.

Висновок: щоб повернути двері, потрібен момент, що крутить, певного значення. Чим більше плече сили, тим менше значення сили, яку треба прикласти — навпаки. Тому нам легше штовхати двері там, де плече сили більше.

Схожа історія з гайковим ключем. Щоб закрутити гайку, потрібно взятися за ручку подалі від гайки. За рахунок збільшення плеча ми зменшуємо значення сили, яку слід докласти.

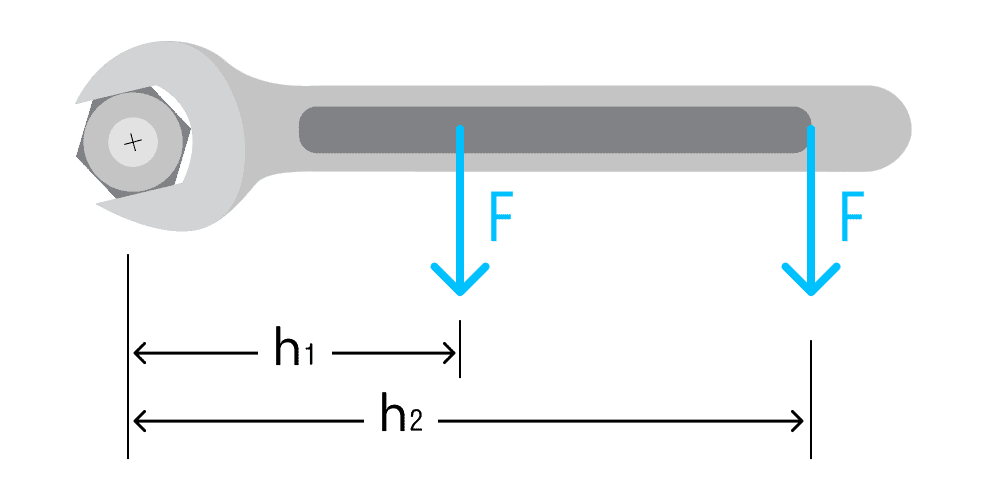
Розрахунок моменту сили

Зараз розглянемо кілька варіантів того, як момент може розраховуватися. За ідеєю просто потрібно помножити силу на плече, але оскільки ми маємо справу з векторами, все не так просто.

Якщо сила розташована перпендикулярно до осі стрижня, ми просто примножуємо модуль сили на плече.

Відстань між точками A і B — 3 метри.

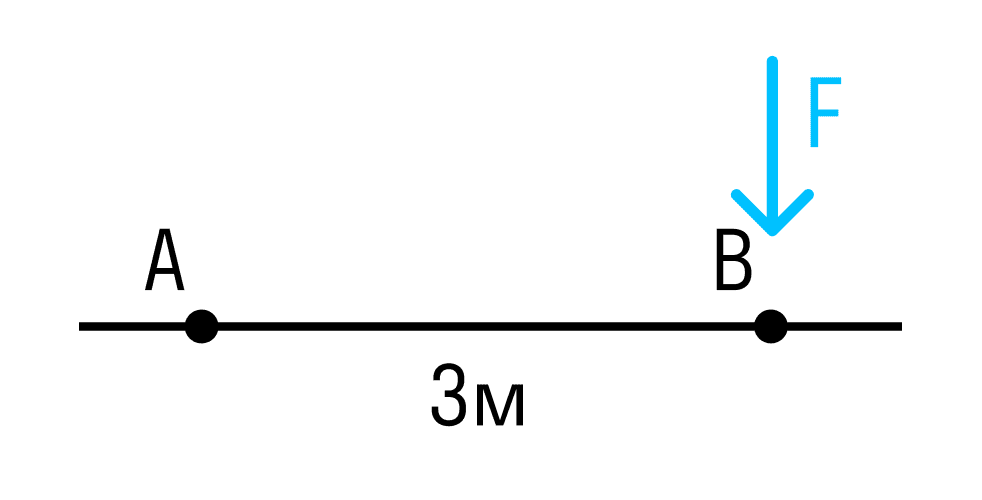
Момент сили щодо точки A:

МА=F×AB=F×3м

Якщо сила розташована під кутом до осі стрижня, множимо проекцію сили на плече.

Зверніть увагу, що такі завдання можуть зустрітися тільки в учнів не раніше 9 класу!

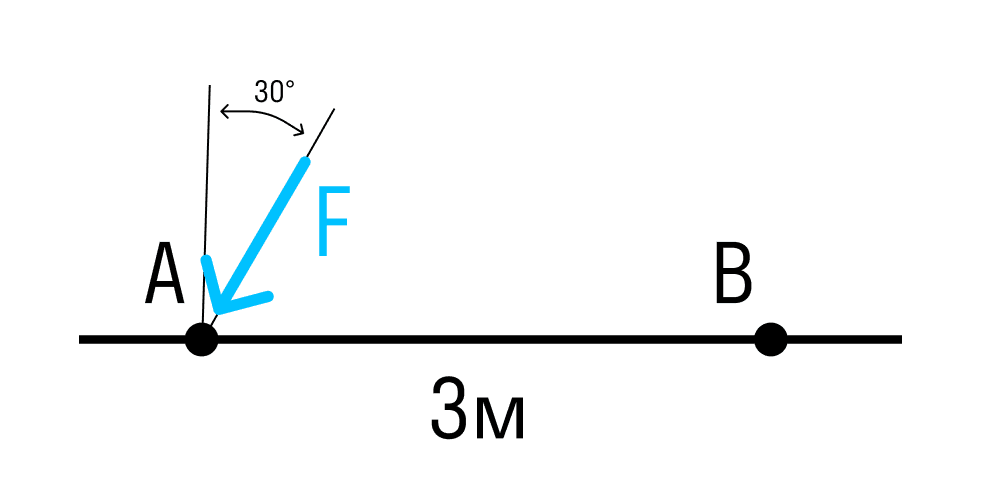
Момент сили щодо точки B:

MB =F×cos30×AB=F×cos30×3м

Якщо відома найкоротша відстань від точки до лінії дії сили, момент розраховується як добуток сили на цю відстань (плечо).

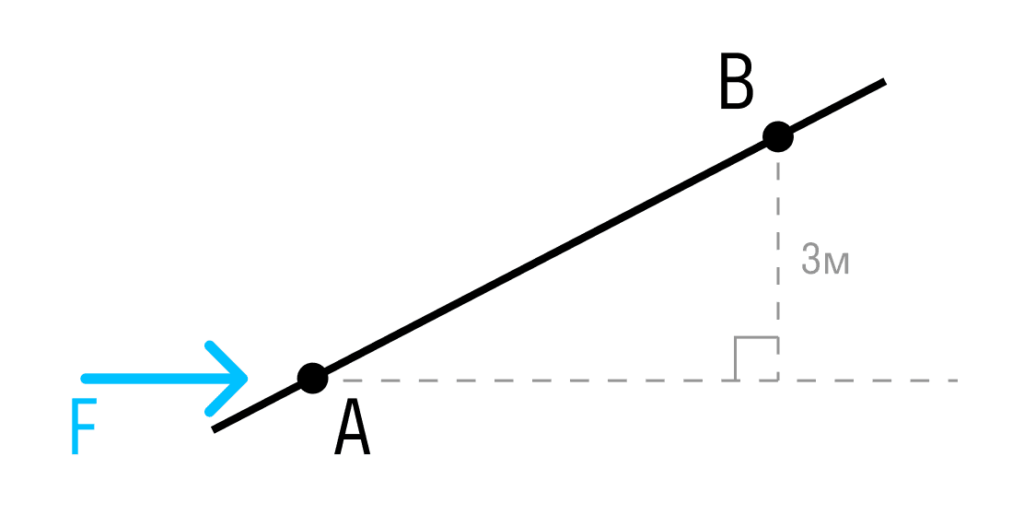
Момент сили щодо точки B:

MB=F×3м

Правило моментів

Повернемося до наших ~~баранів~~ гойдалки. Сили, з якими ми діємо на різні боки цих гойдалок можуть бути різними, але моменти повинні бути однаковими.

Правило моментів говорить про те, що якщо важіль не обертається, то сума моментів сил, що повертають важіль проти годинникової стрілки, дорівнює сумі моментів сил, що повертають важіль за годинниковою стрілкою.

Ця умова виконується відносно будь-якої точки.

Правило моментів
M₁ + M₂ +…+ M_n = M’₁ + M’₂ +…+ M’_n
M₁ + M₂+…+ M_n — сума моментів сил, що повертають важіль за годинниковою стрілкою [Н*м]
M’₁ + M’₂ +…+ M’_n — сума моментів сил, що повертають важіль проти годинникової стрілки [Н*м]

Давайте розглянемо цей закон на прикладі завдань.

Завдання 1

До лівого кінця невагомого стрижня прикріплений вантаж масою 3 кг.

Стержень розташували на опорі, що віддалена від його лівого кінця на 0,2 довжини стрижня. Чому дорівнює маса вантажу, який треба підвісити до правого кінця стрижня, щоб він був у рівновазі?

Рішення:

Однією з умов рівноваги стрижня є те, що повний момент усіх зовнішніх сил щодо будь-якої точки дорівнює нулю. Розглянемо моменти сил щодо точки опори. Момент, створюваний лівим вантажем дорівнює він крутить стрижень проти годинникової стрілки. Момент, створюваний правим вантажем:

Mg\frac{4L}{5}— він  обертає  по г одиннику.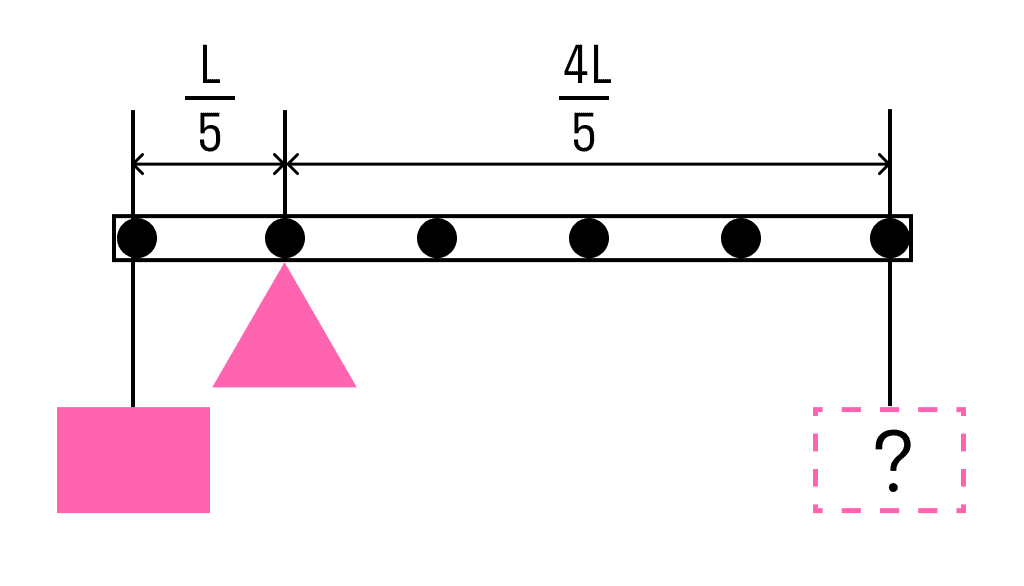

Прирівнюючи моменти, отримуємо, що для рівноваги до правого кінця стрижня необхідно підвісити вантаж масою

M = m : 4 = 3 : 4 = 0,75 кг

Відповідь: для рівноваги до правого кінця стрижня необхідно підвісити вантаж масою 0,75 кг

Завдання 2

Мандрівник несе мішок з речами на легкій палиці. Щоб утримати в рівновазі вантаж вагою 80 Н, він прикладає до кінця B палиці вертикальну силу 30 Н. OB = 80 см. Чому дорівнює OA?

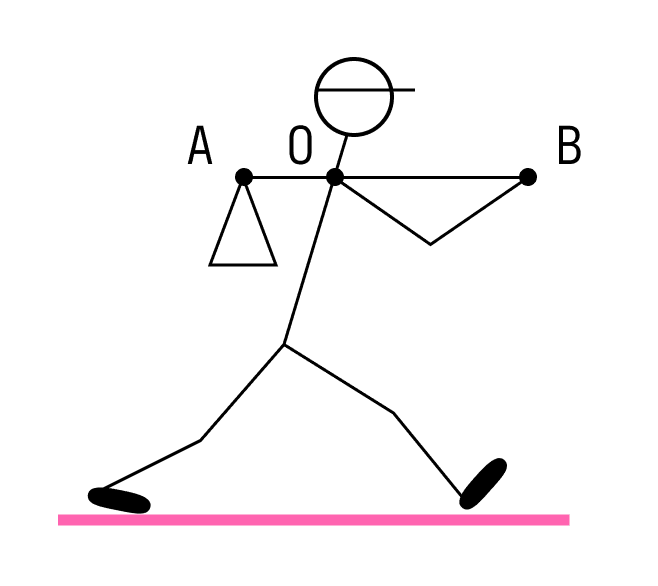
Рішення :

За правилом важеля:

\frac{F_B}{F_A}=\frac{|OA|}{|OB|}

де FA і FB — сили, прикладені відповідно до точок A і B. Виразимо довжину OA:

|OA|=\frac{F_B}{F_A}*|OB|=\frac{30}{80}*80=30 см

Відповідь: відстань ОА дорівнює 30 см

Завдання 3

Тіло масою 0,2 кг підвішене до правого плеча невагомого важеля (див. малюнок) ). Вантаж якої маси треба підвісити до другого поділу лівого плеча важеля для досягнення рівноваги?

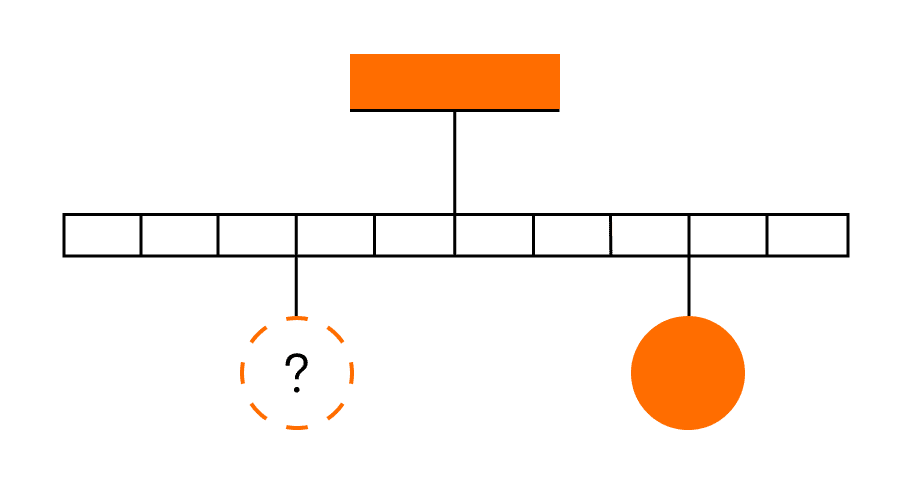
Рішення:

За правилом важеля

m_1g*l_1=m_2g*l_2

Звідси

m_2=\frac{l_1}{l_2}m_1=\frac{3}{2}*0,2=0,3 кг

Відповідь : Маса вантажу дорівнює 0,3 кг.

Завдання 4 – a.k.a найскладніше завдання

Під дією сили тяжіння mg вантажу і сили F важіль, представлений на малюнку, знаходиться в рівновазі. Вектор сили F перпендикулярний до важеля, вантаж на площину не тисне. Відстань між точками докладання сил і точкою опори, а також проекції цих відстаней на вертикальну та горизонтальну осі вказані на малюнку.

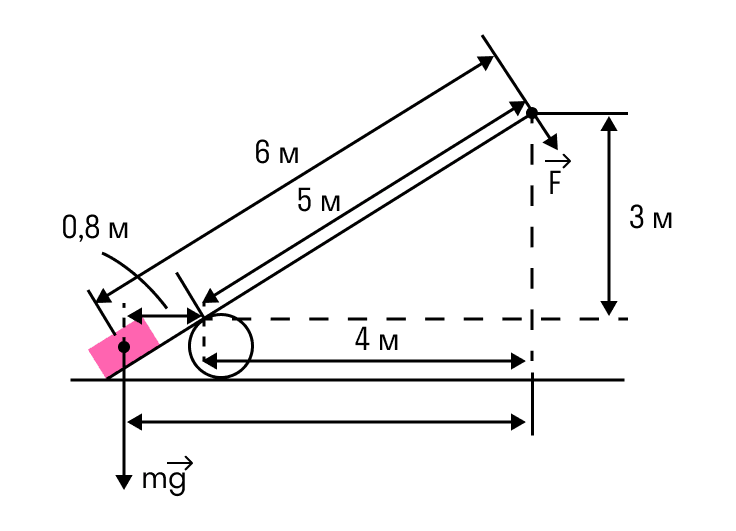
Якщо модуль сили F дорівнює 120 Н, то яким є модуль сили тяжіння, що діє на вантаж?

Рішення:

Однією з умов рівноваги важеля є те, що повний момент усіх зовнішніх сил відносно будь-якої точки дорівнює нулю. Розглянемо моменти сил щодо опори важеля. Момент, створюваний силою F, дорівнює F * 5 м і він обертає важіль за годинниковою стрілкою. Момент, створюваний вантажем щодо цієї точки — mg*0,8 м, він обертає проти вартовий. Уточнимо, що 0,8 м – це відстань від центру ваги вантажу до опори, тобто перпендикуляр до осі обертання. Прирівнюючи моменти, отримуємо вираз для модуля сили тяжіння